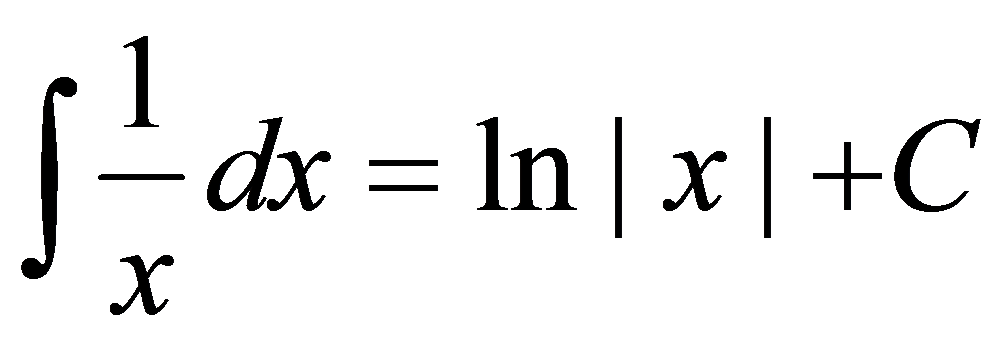4.1.1 原函数与不定积分的概念
4.1.1 原函数与不定积分的概念
定义4.1.1设函数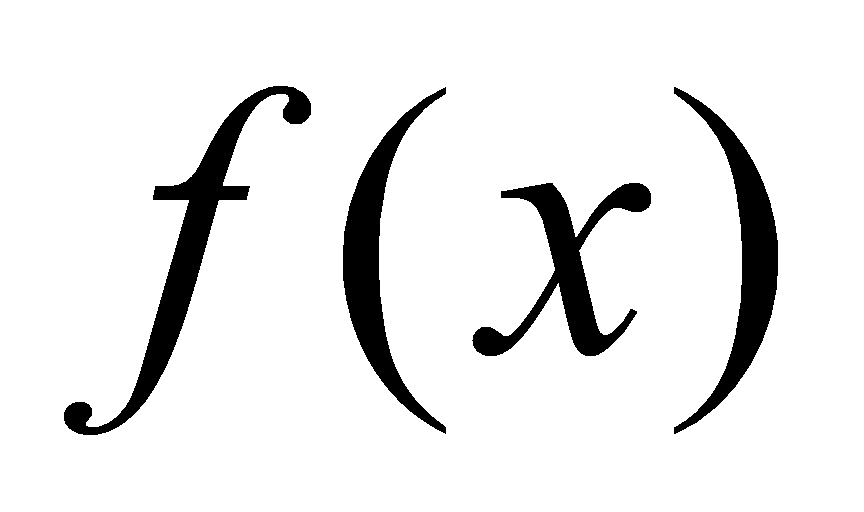 与
与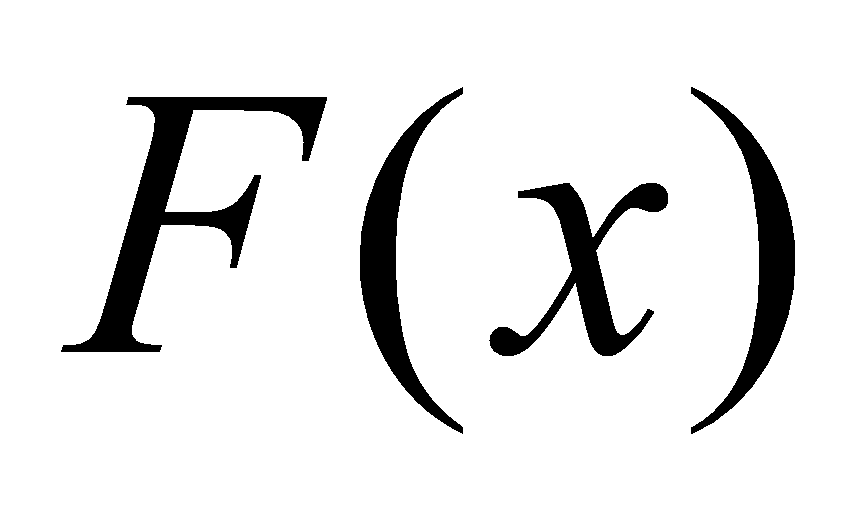 在区间
在区间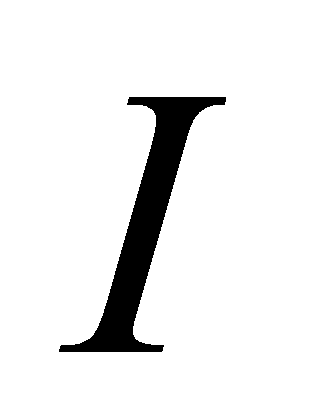 上有定义。若
上有定义。若
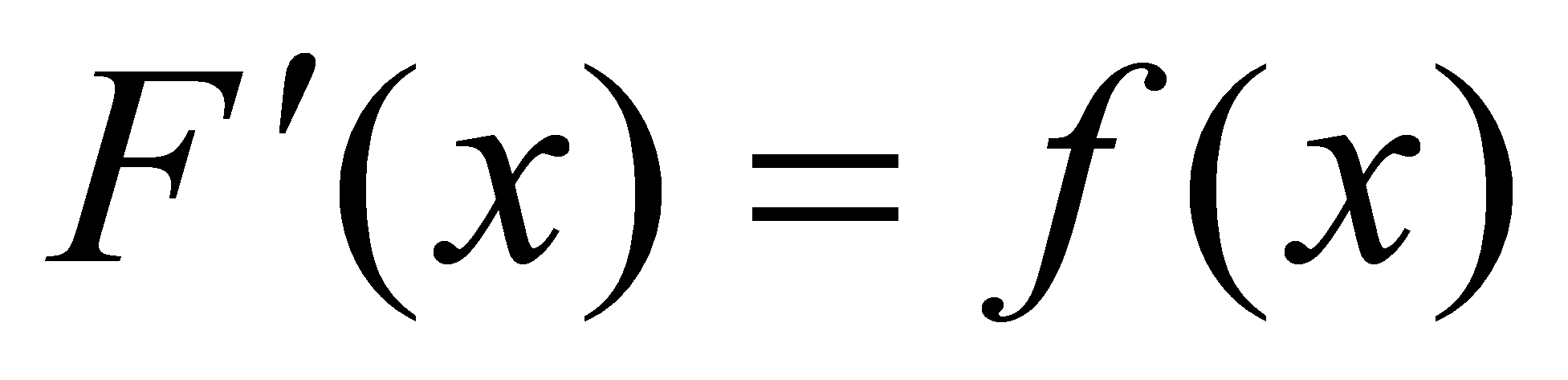 ,
, 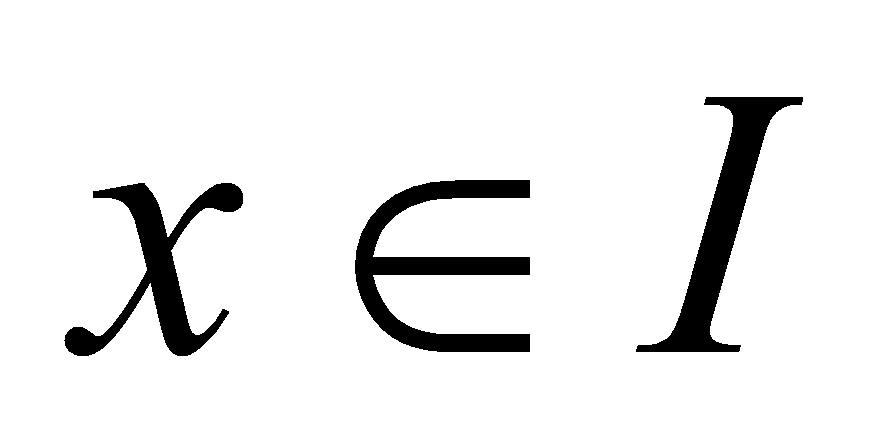 ,
,
则称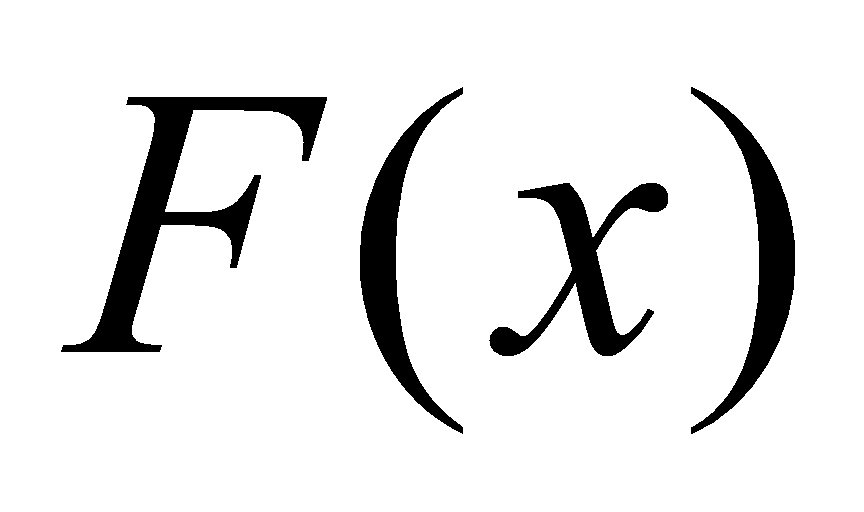 为
为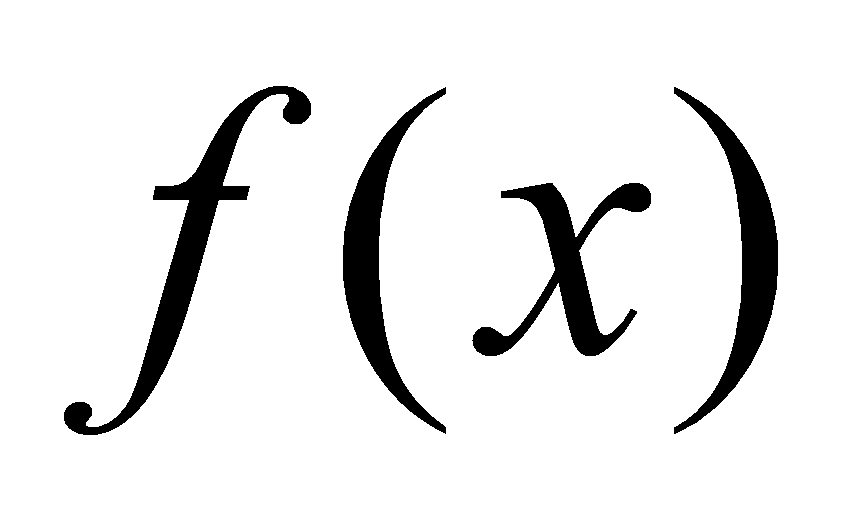 在区间
在区间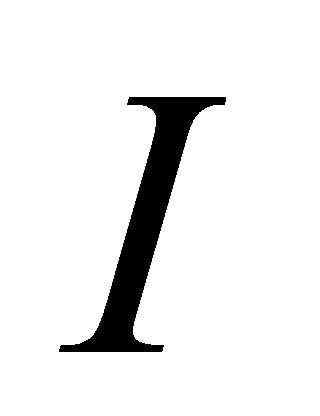 上的一个原函数(primitive function)。
上的一个原函数(primitive function)。
如: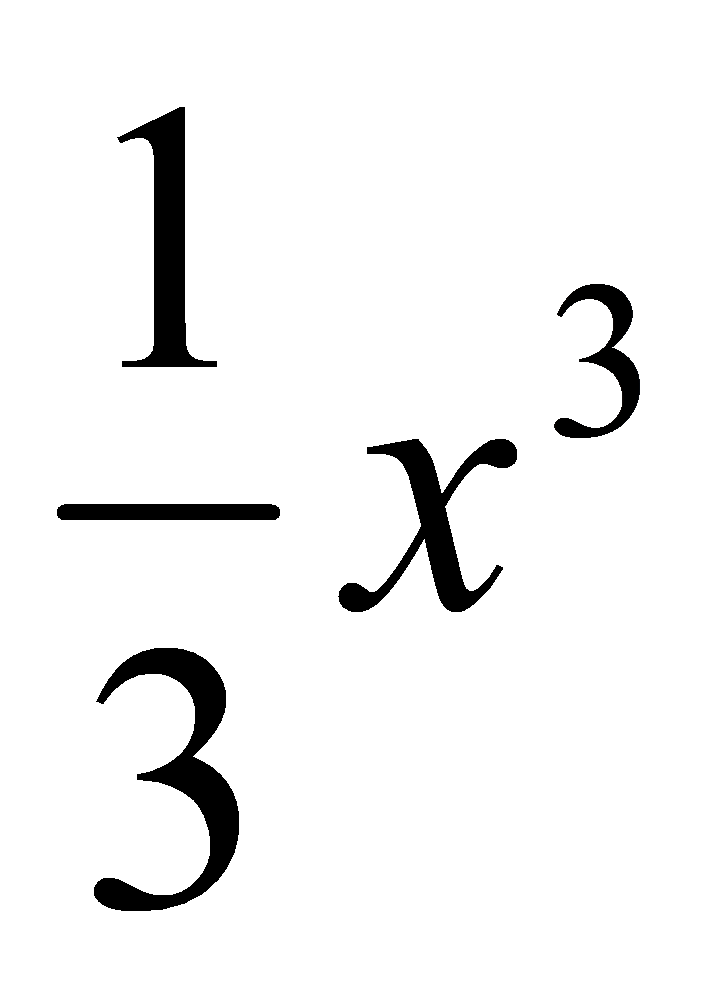 是
是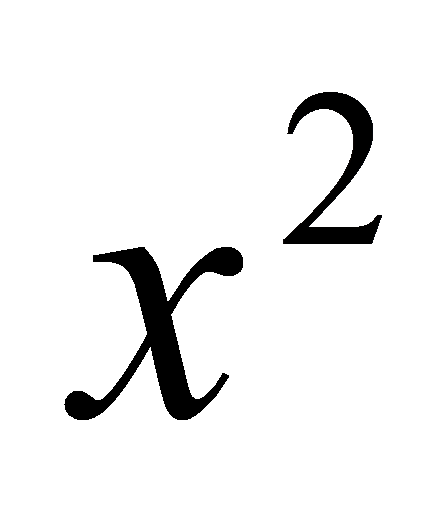 在R上的一个原函数;
在R上的一个原函数;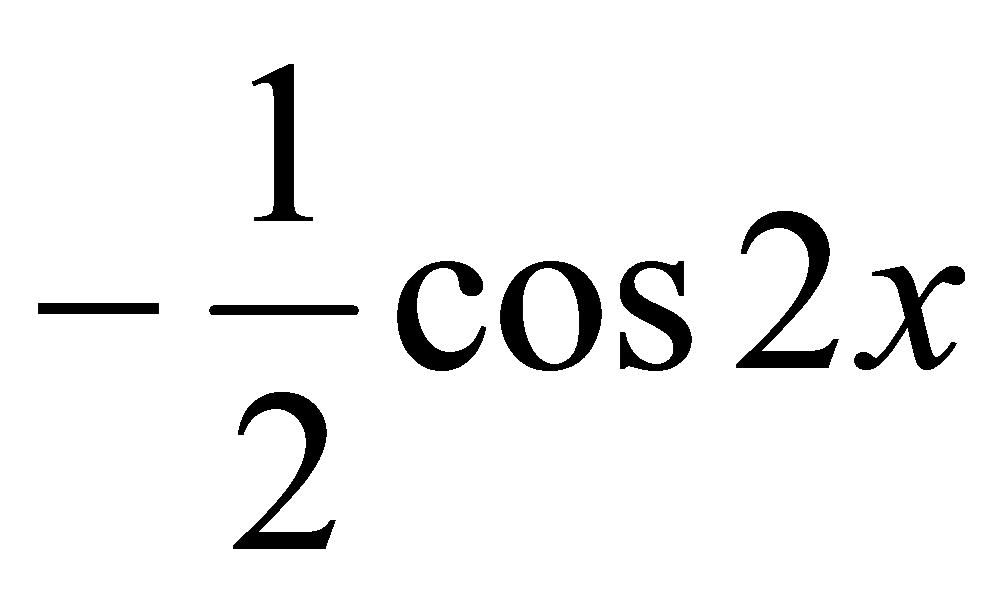 ,
, 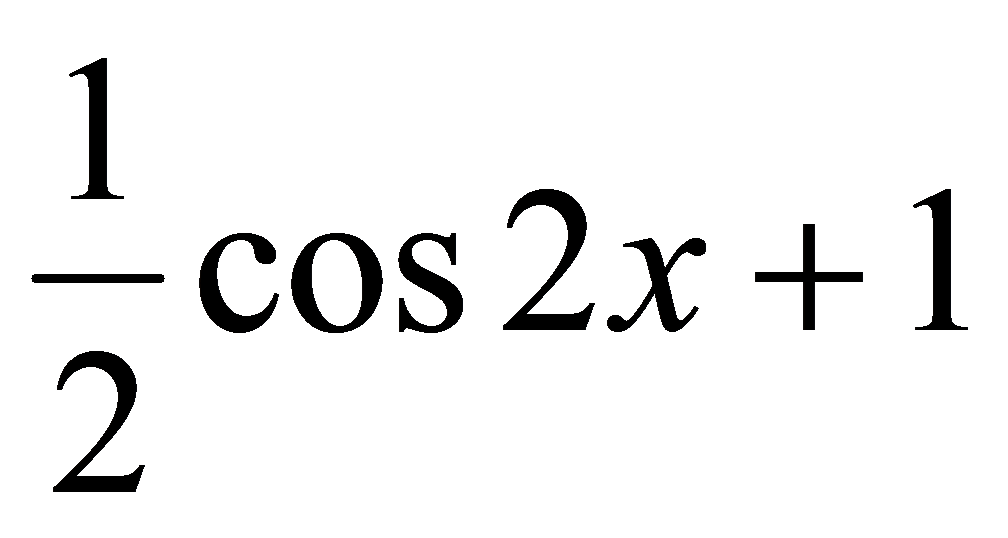 ,
, ,
,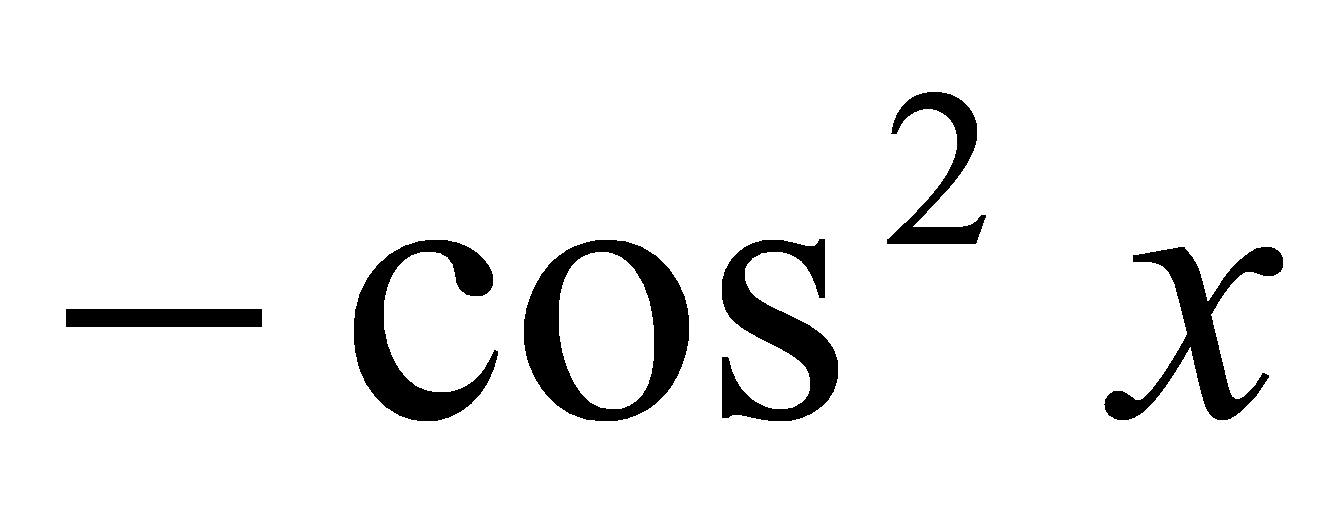 等都有是
等都有是 在R上的原函数——若函数
在R上的原函数——若函数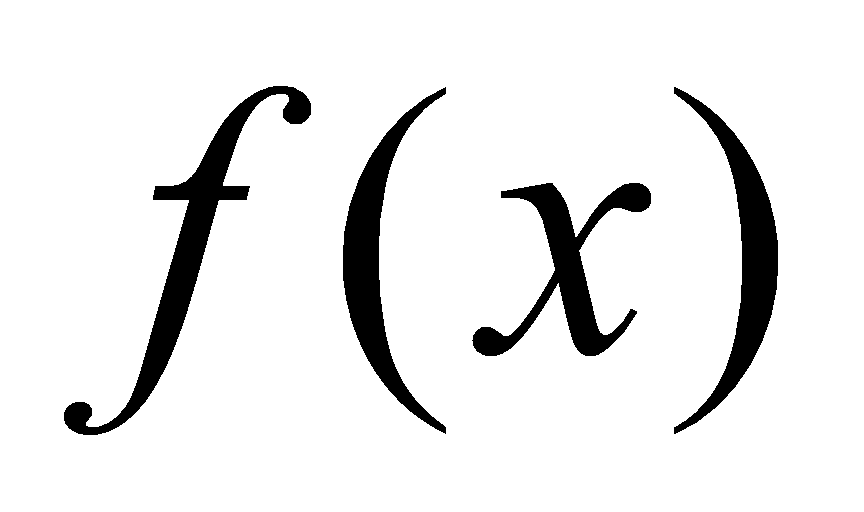 存在原函数,则其原函数不是唯一的。对此我们有:
存在原函数,则其原函数不是唯一的。对此我们有:
定理4.1.1设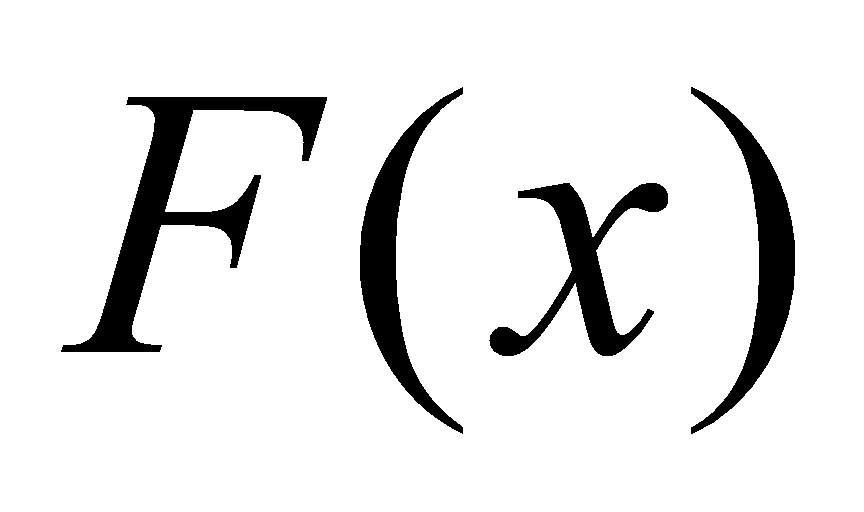 是
是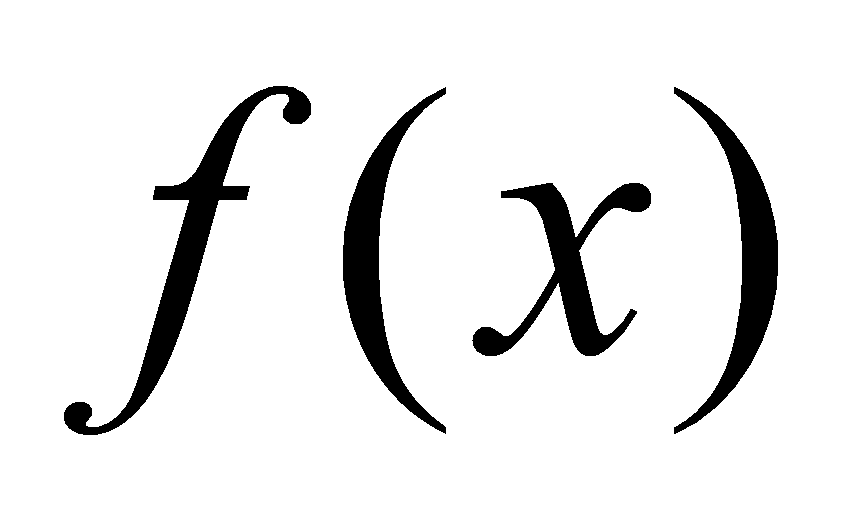 在区间
在区间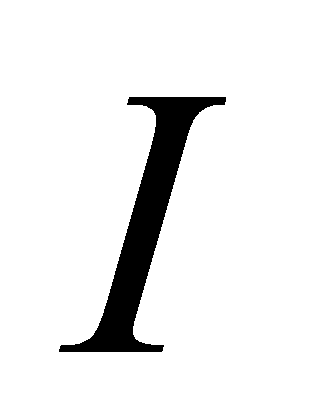 上的一个原函数,则(1)
上的一个原函数,则(1)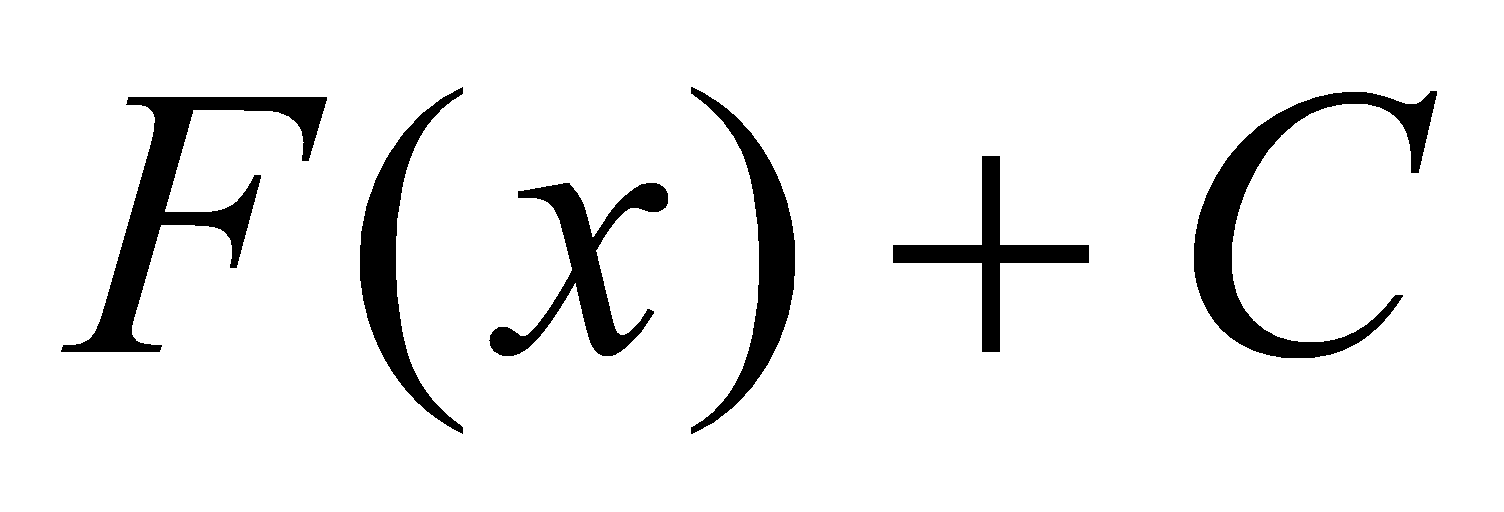 也是
也是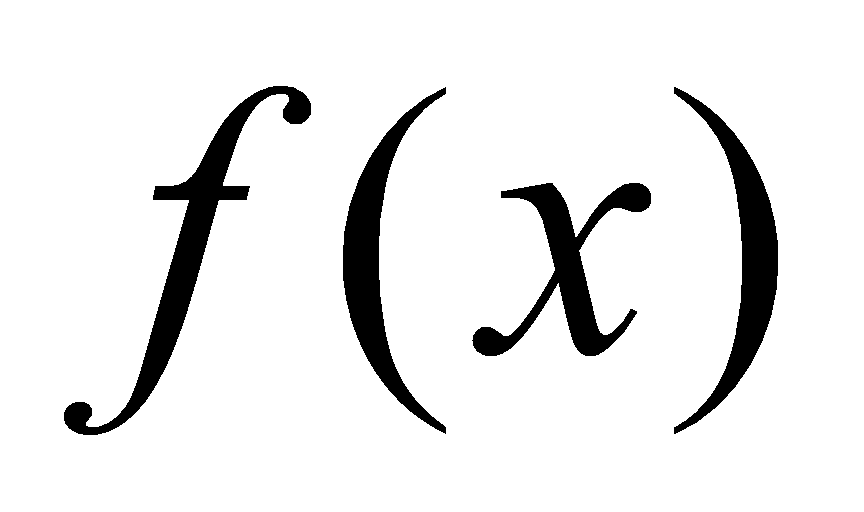 的原函数,其中
的原函数,其中 为任意常数;(2)
为任意常数;(2) 的任意两个原函数之间相差一个常数.
的任意两个原函数之间相差一个常数.
由定理4.1.1(2)可知,如果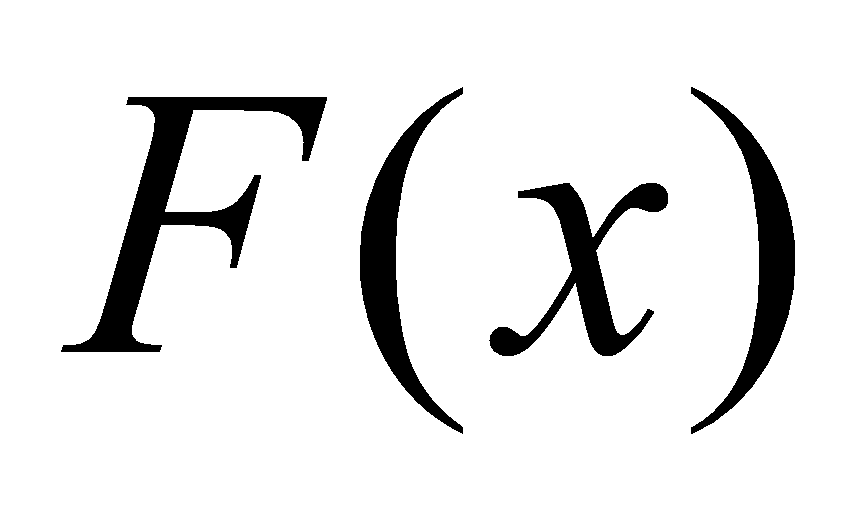 是
是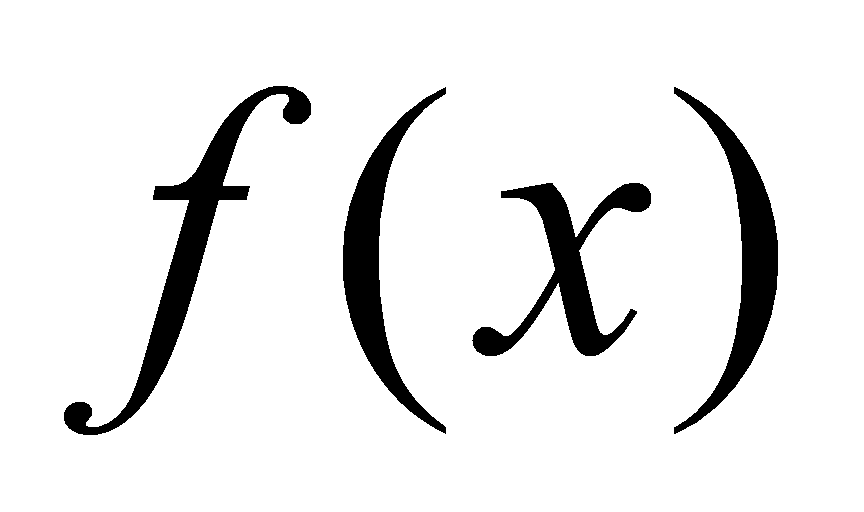 的一个原函数,则
的一个原函数,则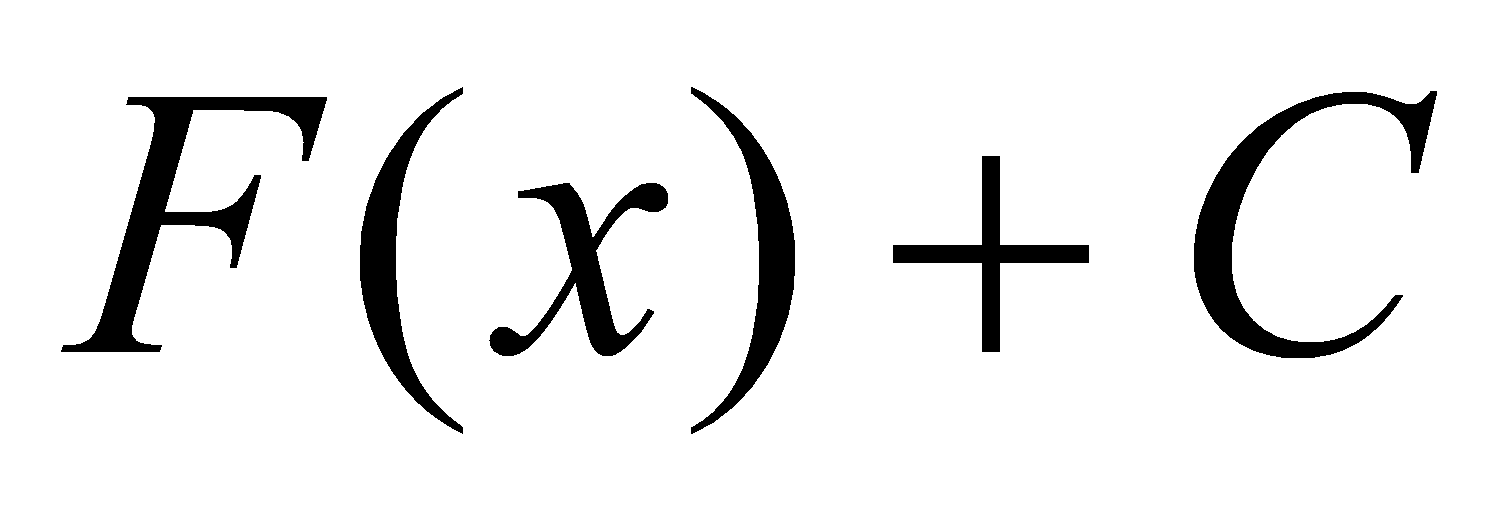 就是
就是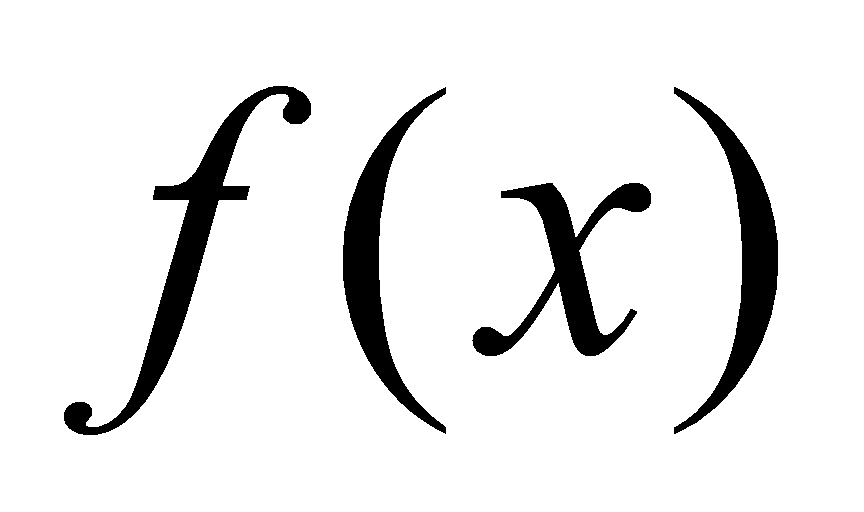 的所有的原函数.这样,如果我们要求函数
的所有的原函数.这样,如果我们要求函数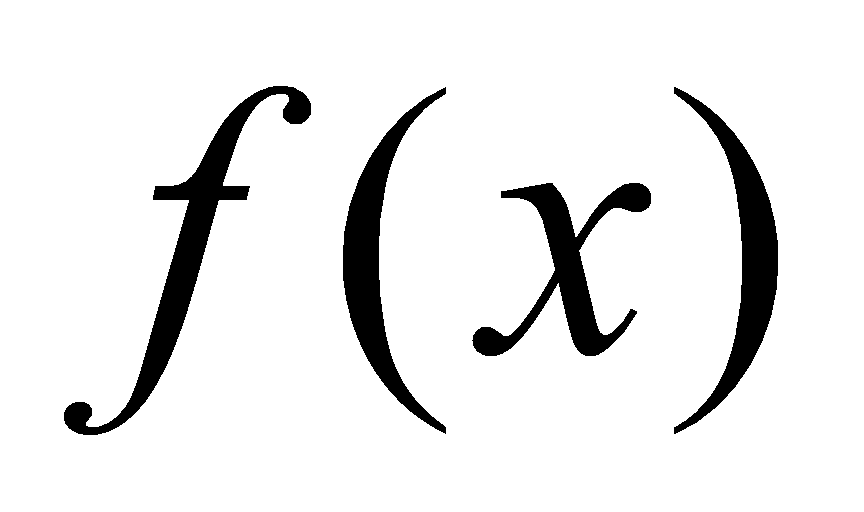 的所有的原函数,只要我们求出
的所有的原函数,只要我们求出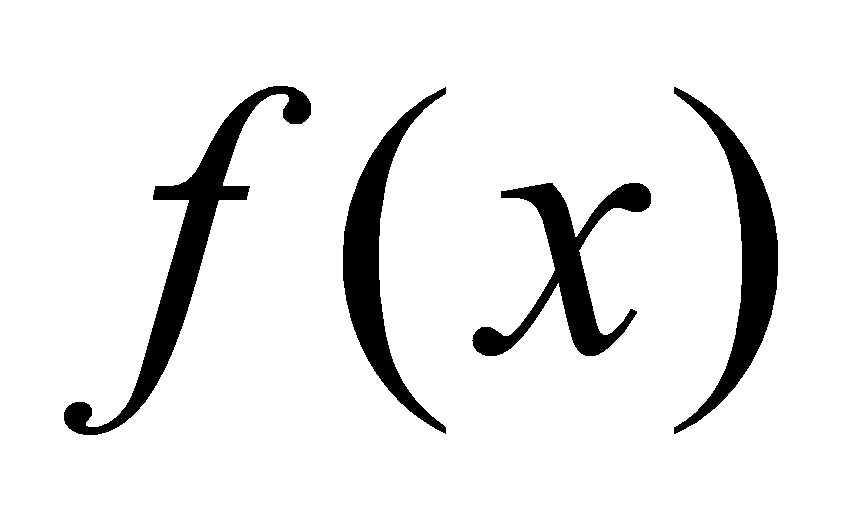 的一个原函数再加上一个任意常数
的一个原函数再加上一个任意常数 就可以了.
就可以了.
另外,对于原函数的存在性问题,我们亦有:
定理4.1.2(原函数存在定理):如果函数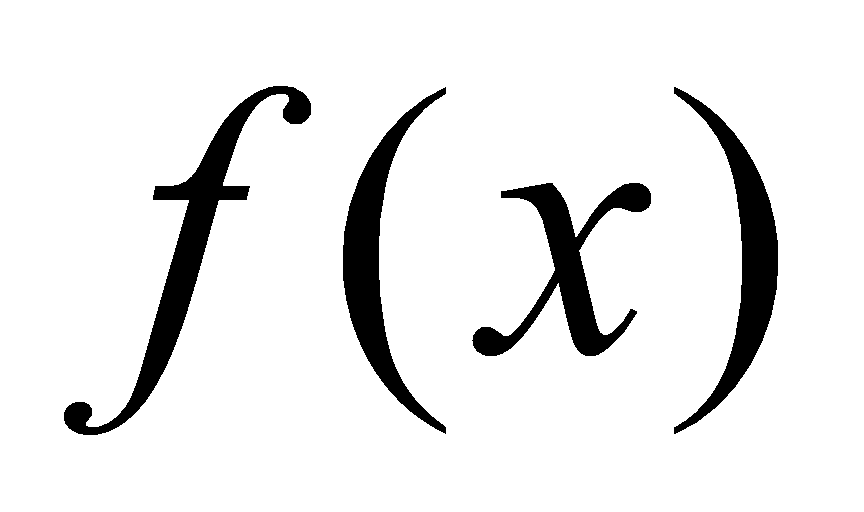 在区间
在区间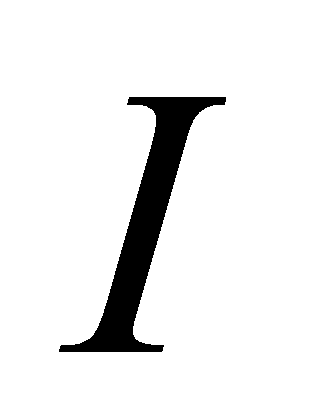 上连续,则
上连续,则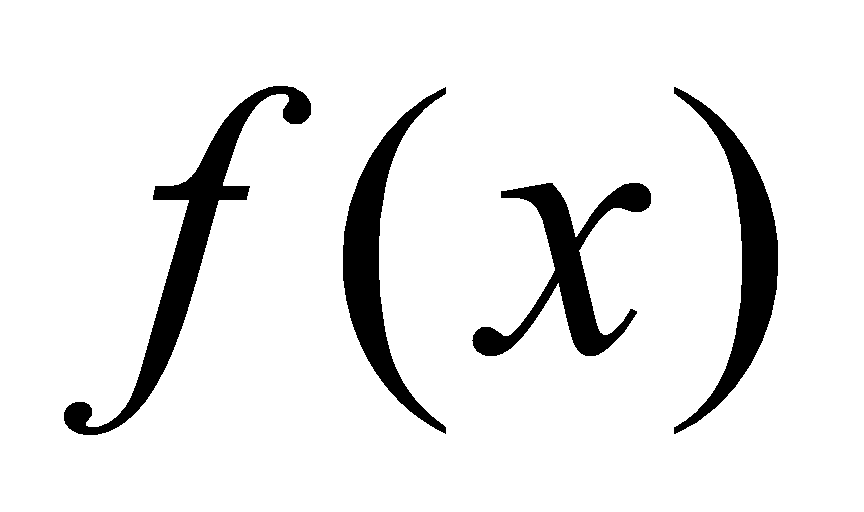 在区间
在区间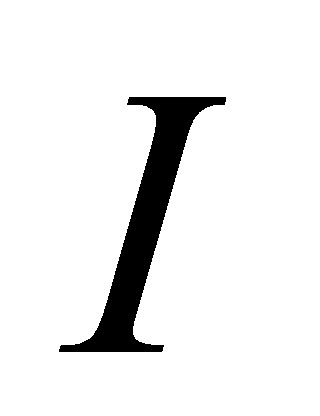 上一定有原函数,即存在区间
上一定有原函数,即存在区间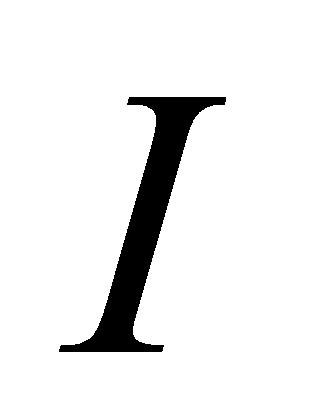 上的可导函数
上的可导函数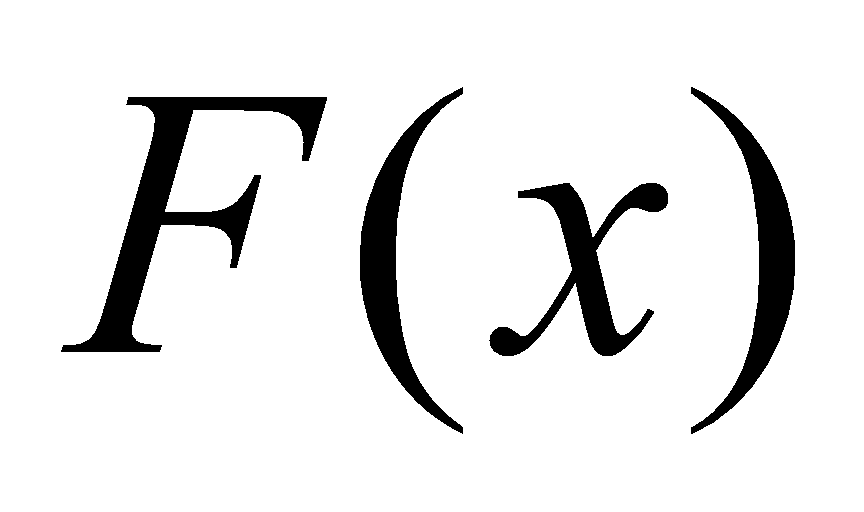 ,使得对任一
,使得对任一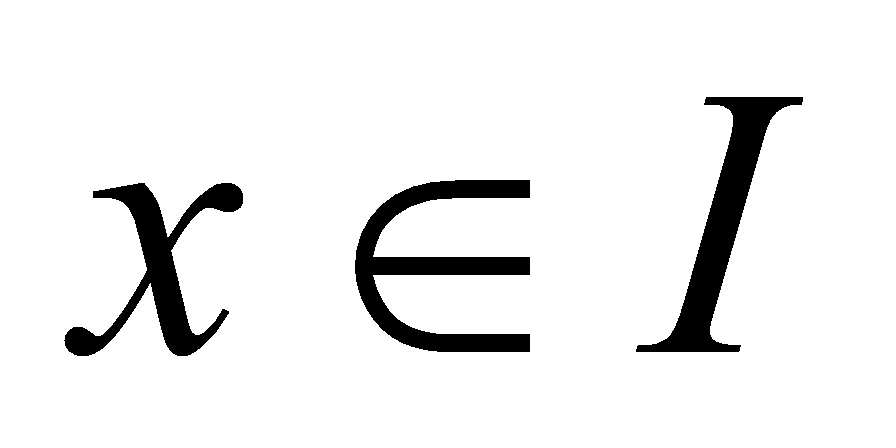 ,有
,有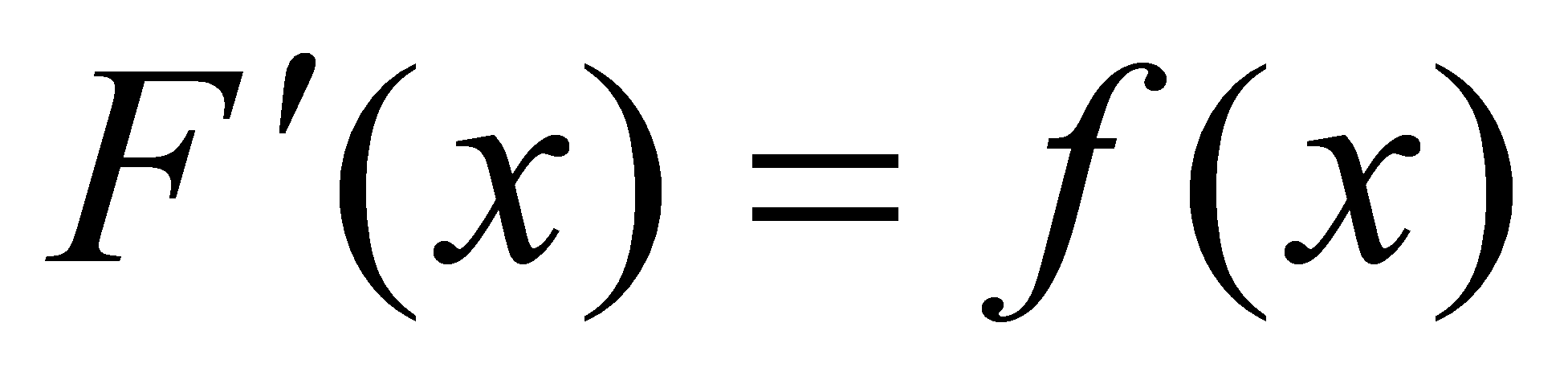 。
。
定义4.1.2函数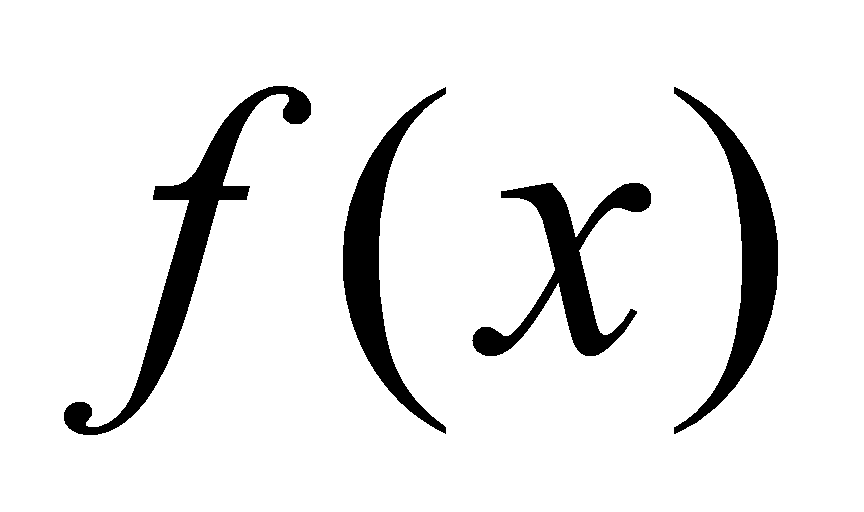 在区间
在区间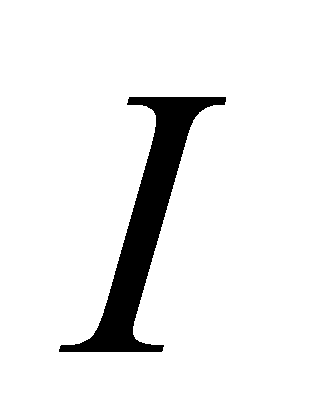 上的全体原函数
上的全体原函数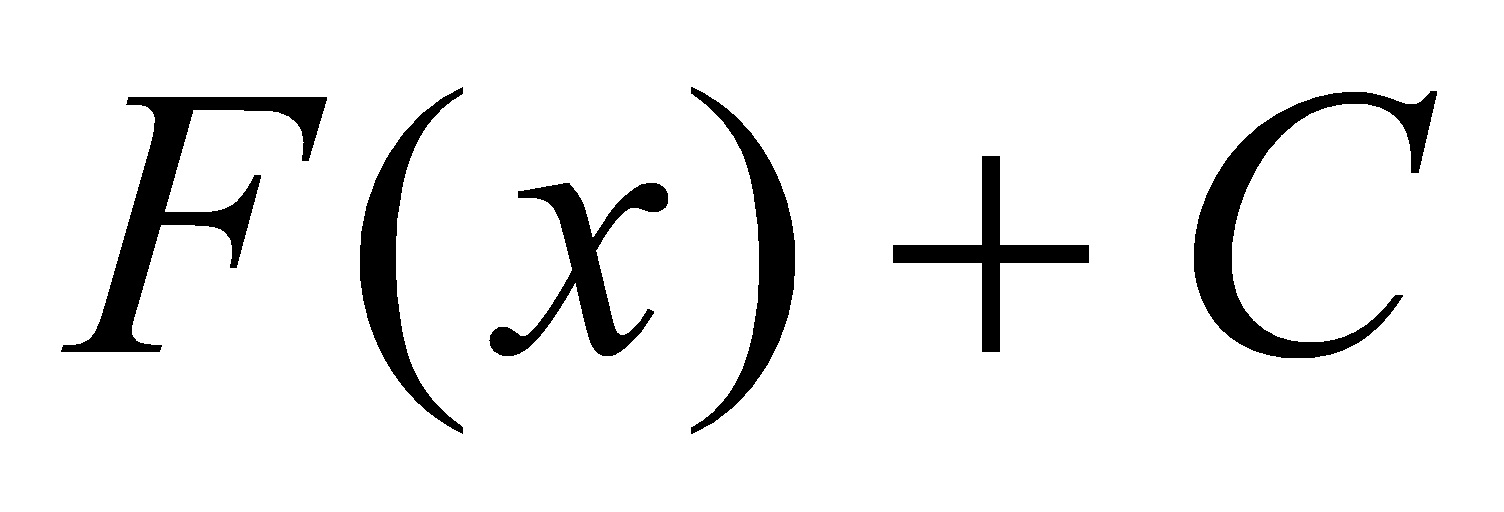 称为函数
称为函数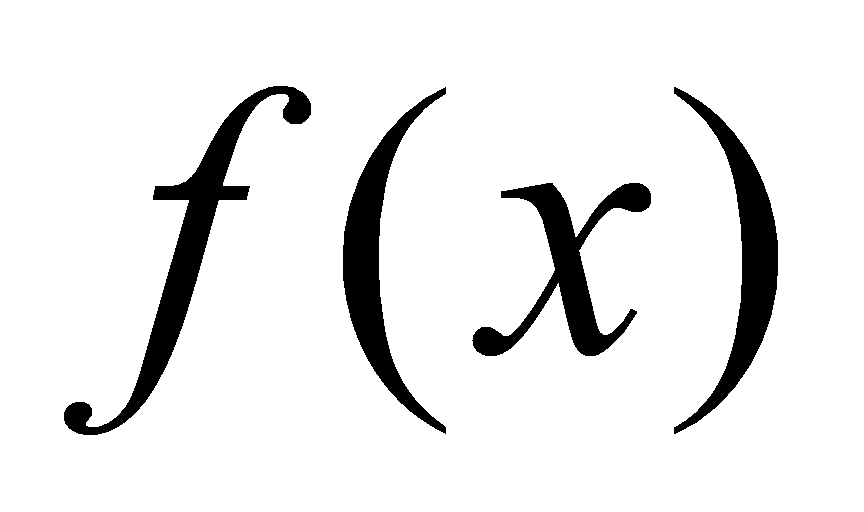 在区间
在区间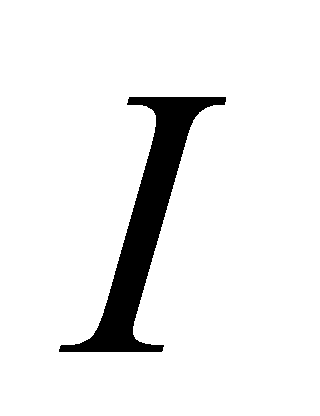 上的不定积分.记为
上的不定积分.记为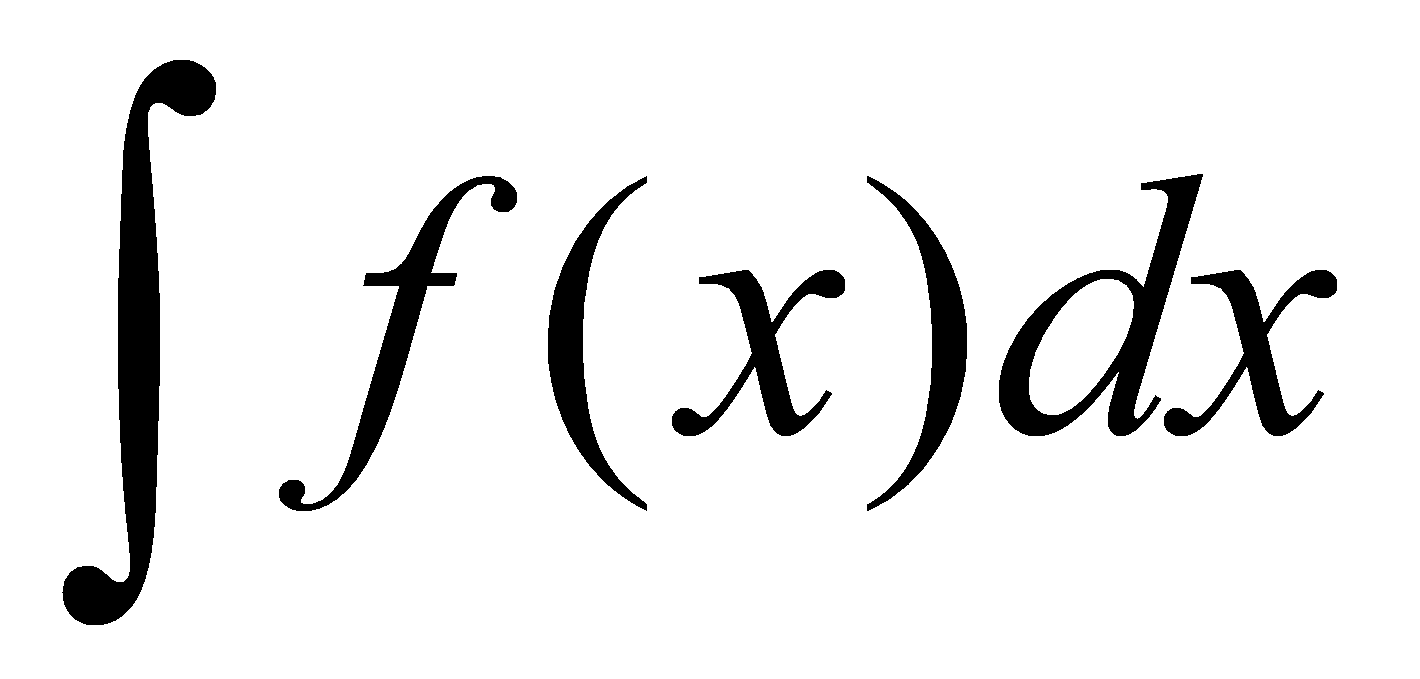 , 即
, 即
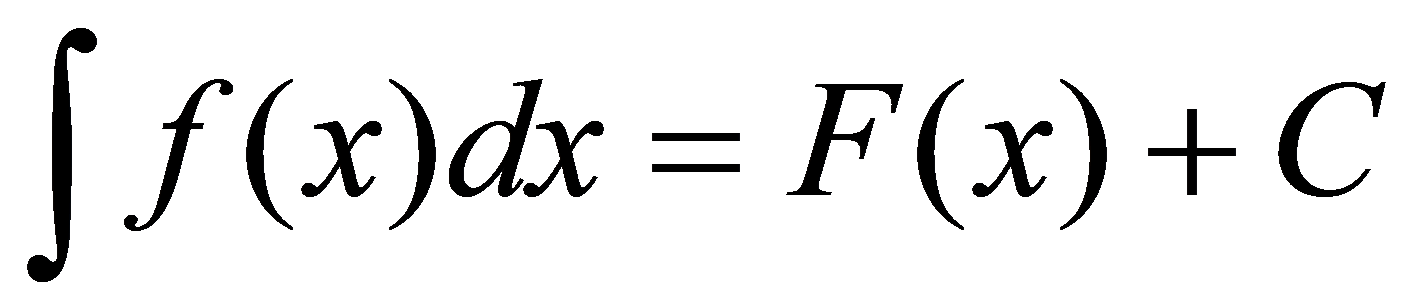 .
.
其中 称为积分号( integrate sign),
称为积分号( integrate sign),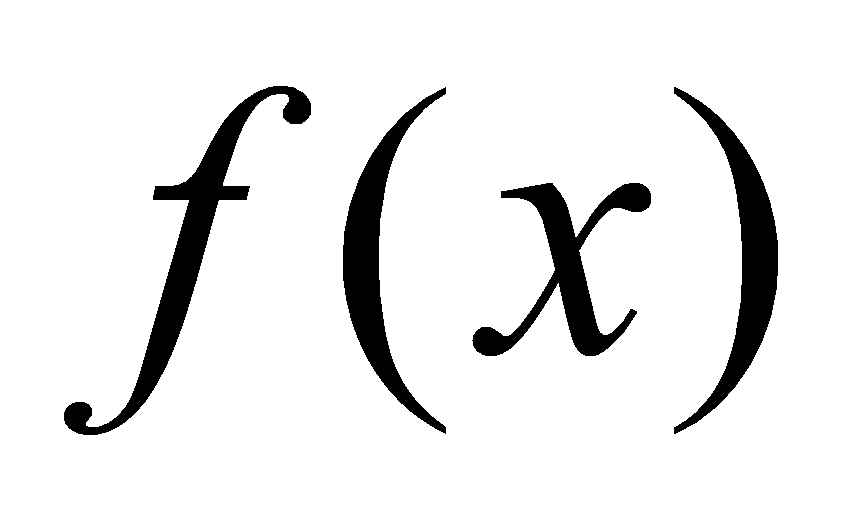 称为被积函数(integrand),
称为被积函数(integrand),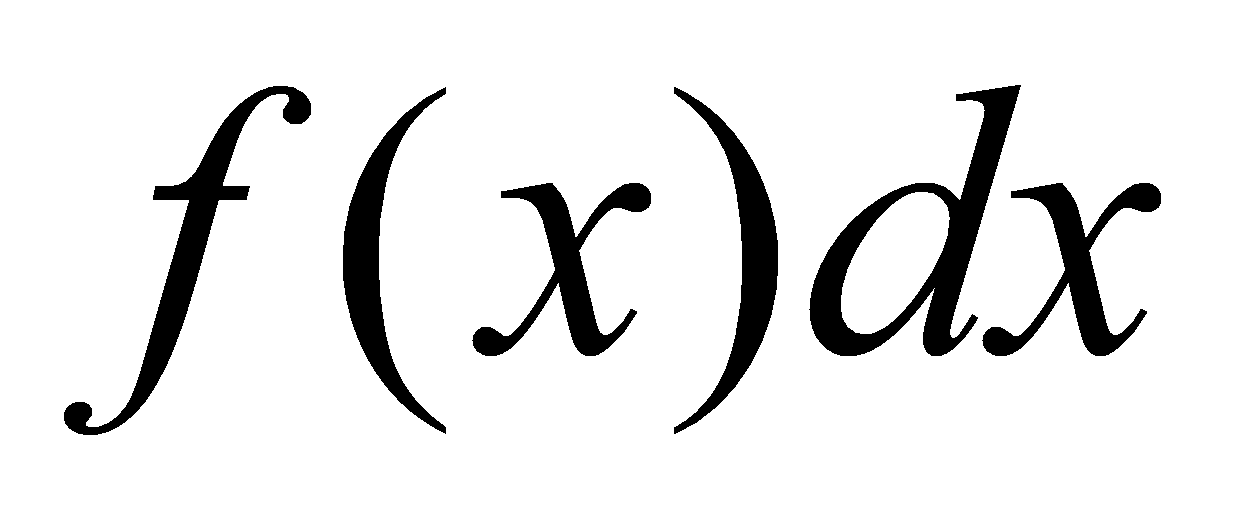 称为被积表达式,
称为被积表达式,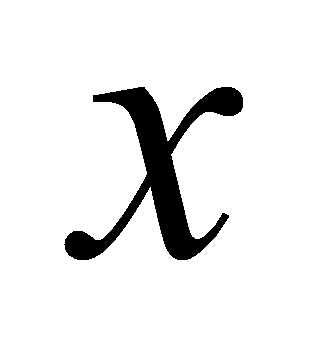 称为积分变量(integral variable),
称为积分变量(integral variable), 称为积分常数(integrationconstant).
称为积分常数(integrationconstant).
由定义4.1.2,有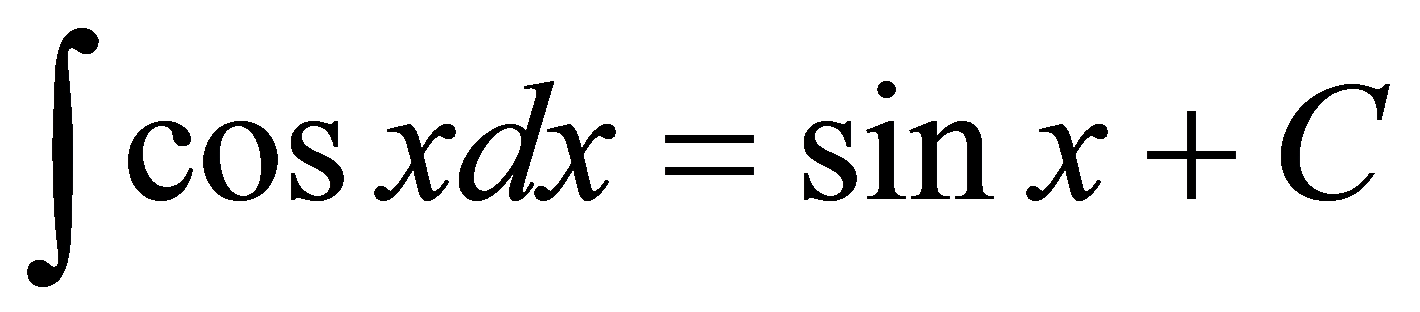 ,
,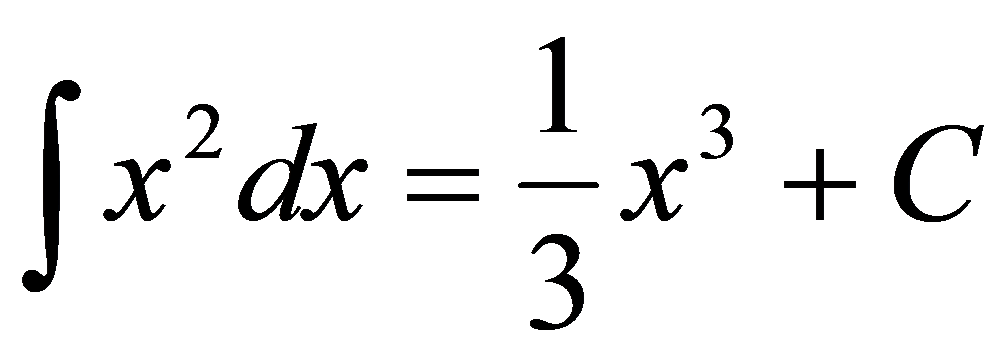 .
.
不定积分的几何意义:如果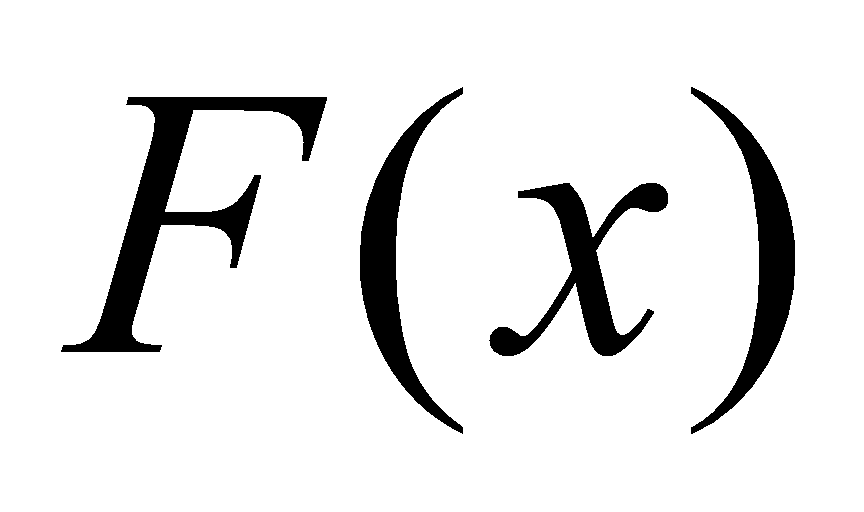 是
是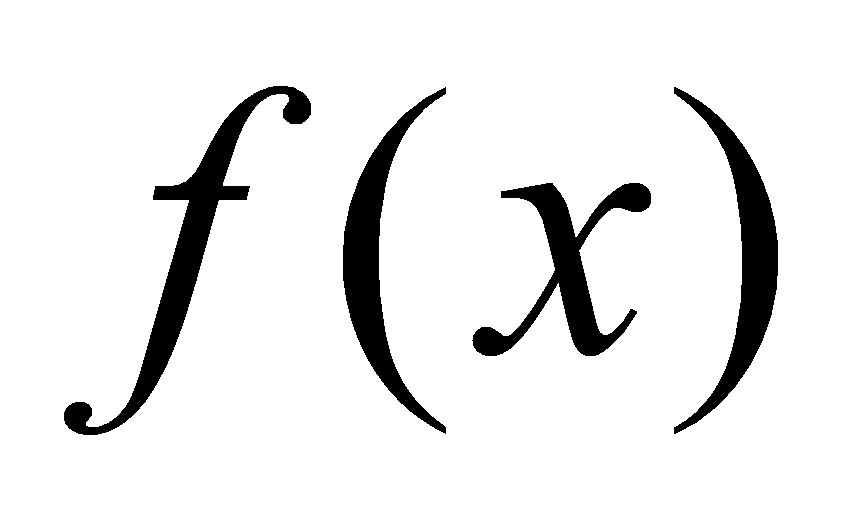 的一个原函数,则
的一个原函数,则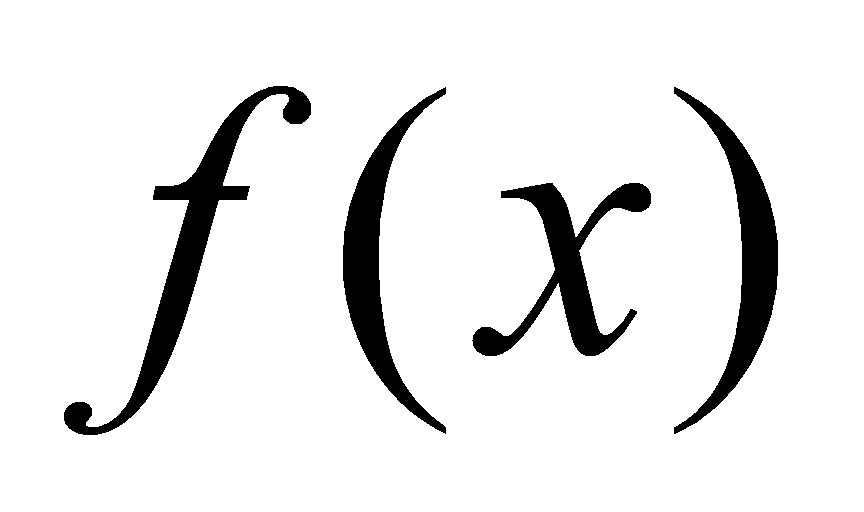 的不定积分
的不定积分 ,对于
,对于 的每一确定的数值,
的每一确定的数值, 表示坐标平面上的一条确定的曲线,这条曲线称为
表示坐标平面上的一条确定的曲线,这条曲线称为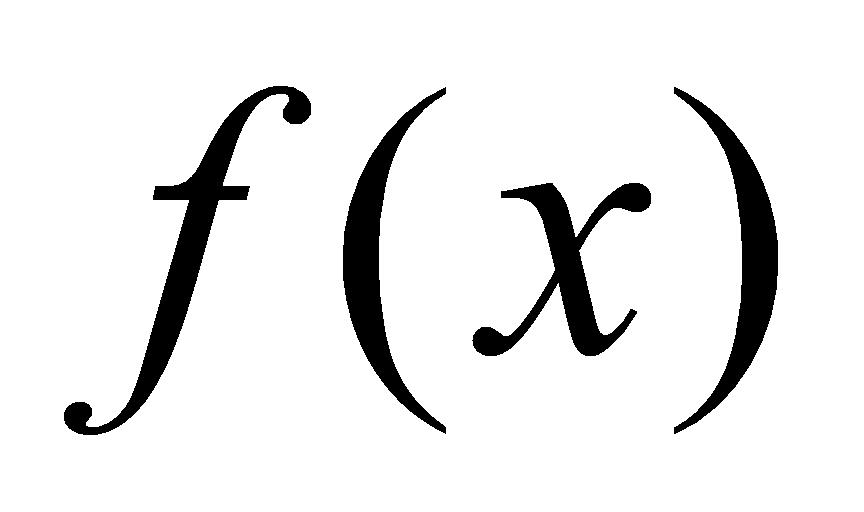 的一条积分曲线(integral curve).由于
的一条积分曲线(integral curve).由于 可以取任意值,因此不定积分
可以取任意值,因此不定积分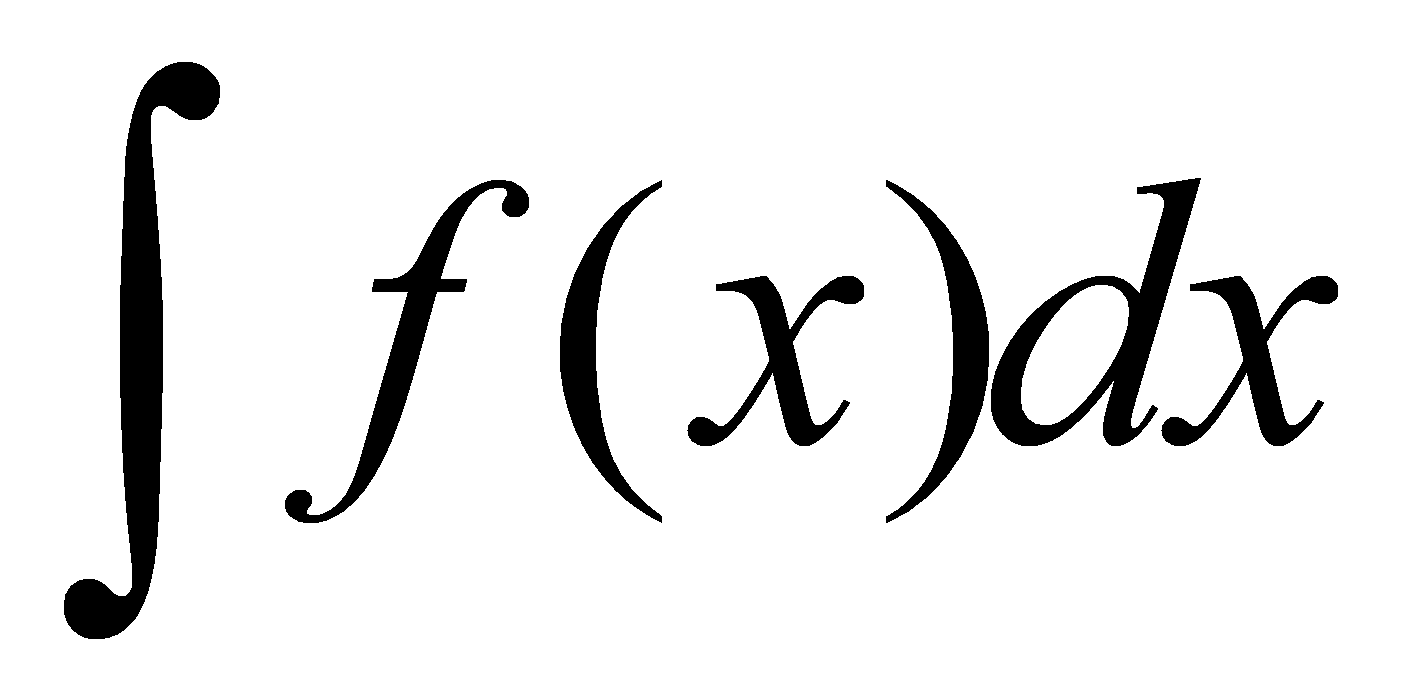 表示
表示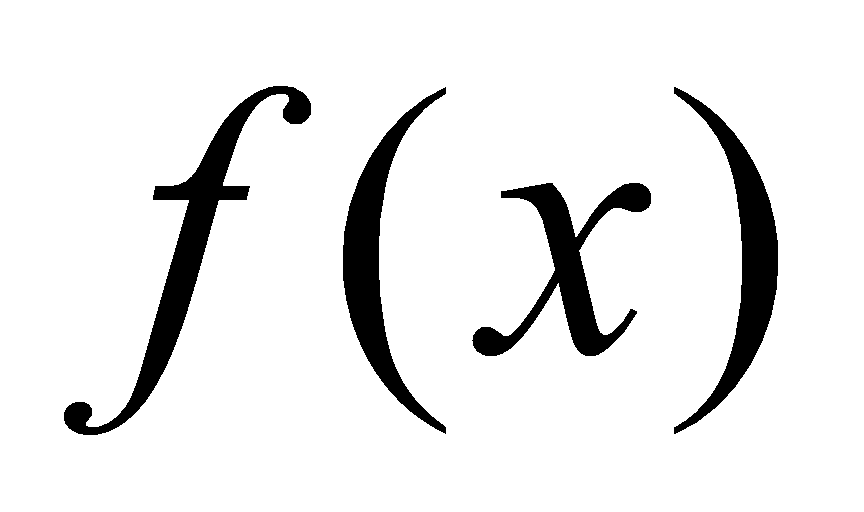 的一族积分曲线,而其中任意一条积分曲线都可以由曲线
的一族积分曲线,而其中任意一条积分曲线都可以由曲线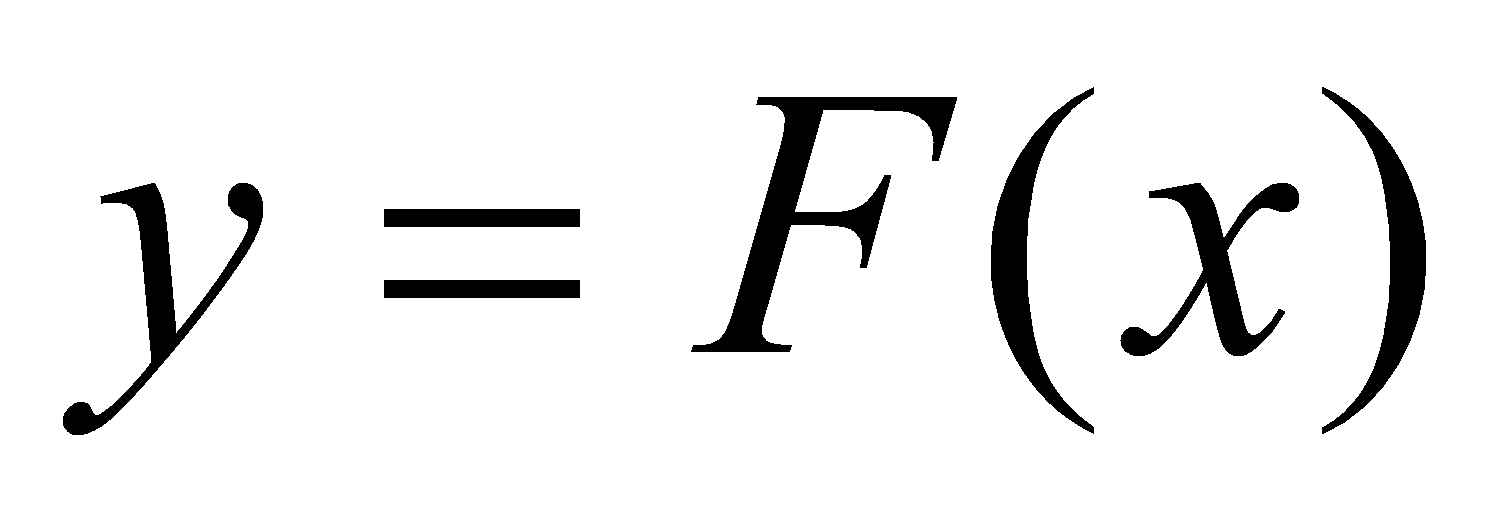 沿
沿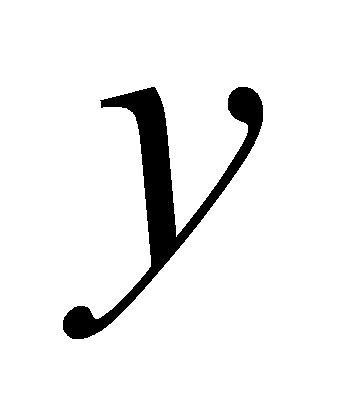 轴方向上、下平移得到.或者说,每一条积分曲线上横坐标相同的点处所作曲线的切线都是互相平行的(图4-1),这就是不定积分的几何意义.
轴方向上、下平移得到.或者说,每一条积分曲线上横坐标相同的点处所作曲线的切线都是互相平行的(图4-1),这就是不定积分的几何意义.
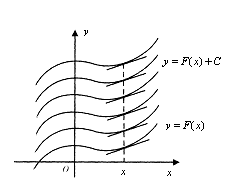
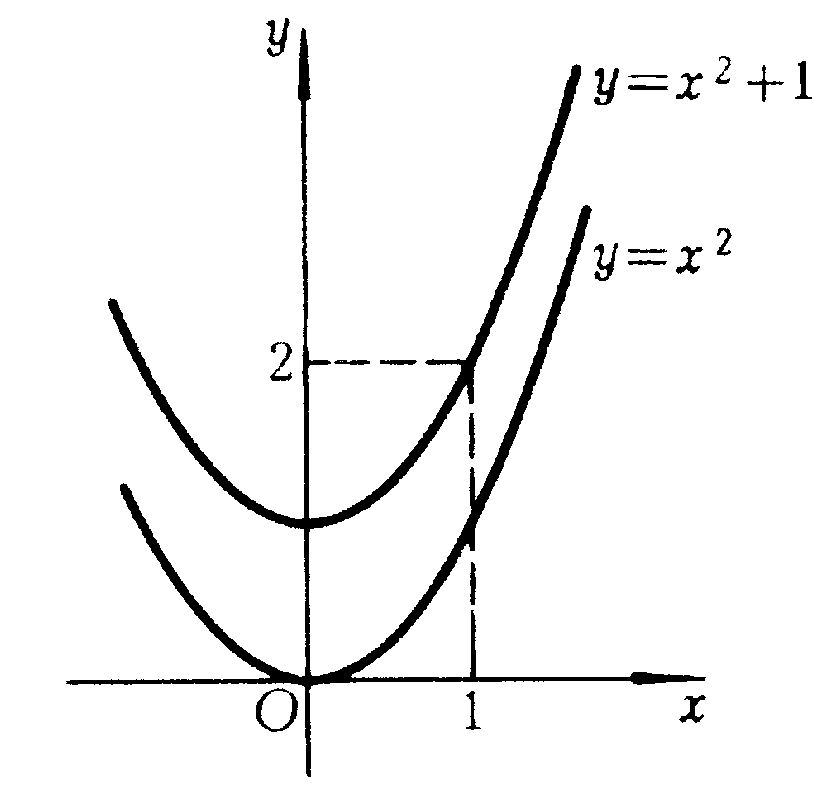
图4-1 图4-2
例4.1.1设曲线通过点(1,2),且曲线上任一点处的切线斜率都是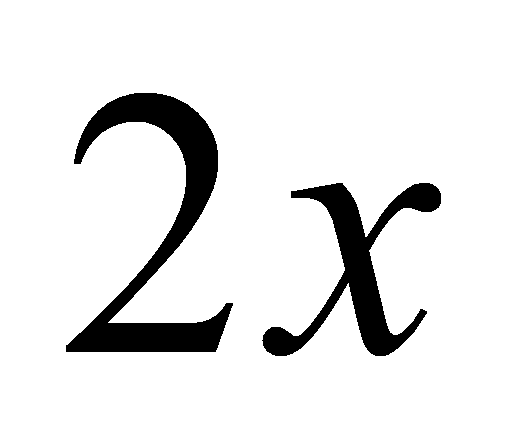 ,求此曲线的方程.
,求此曲线的方程.
解 设该曲线方程为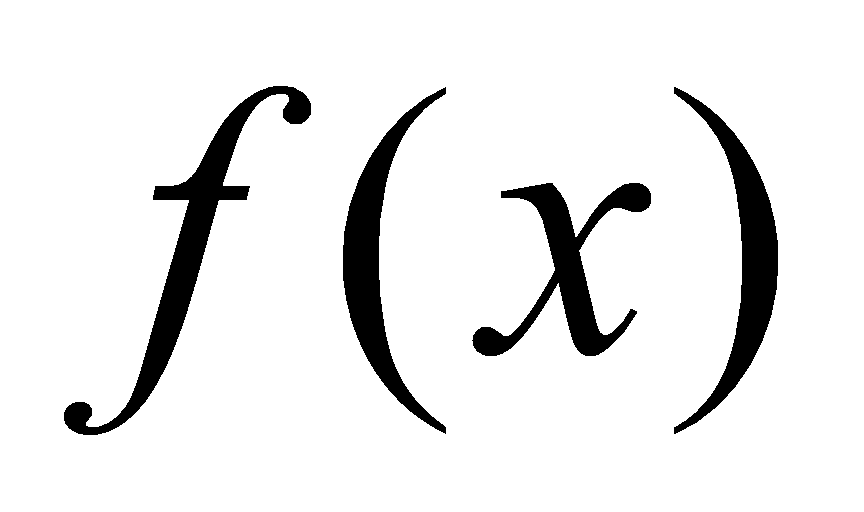 ,则由导数的几何意义,有
,则由导数的几何意义,有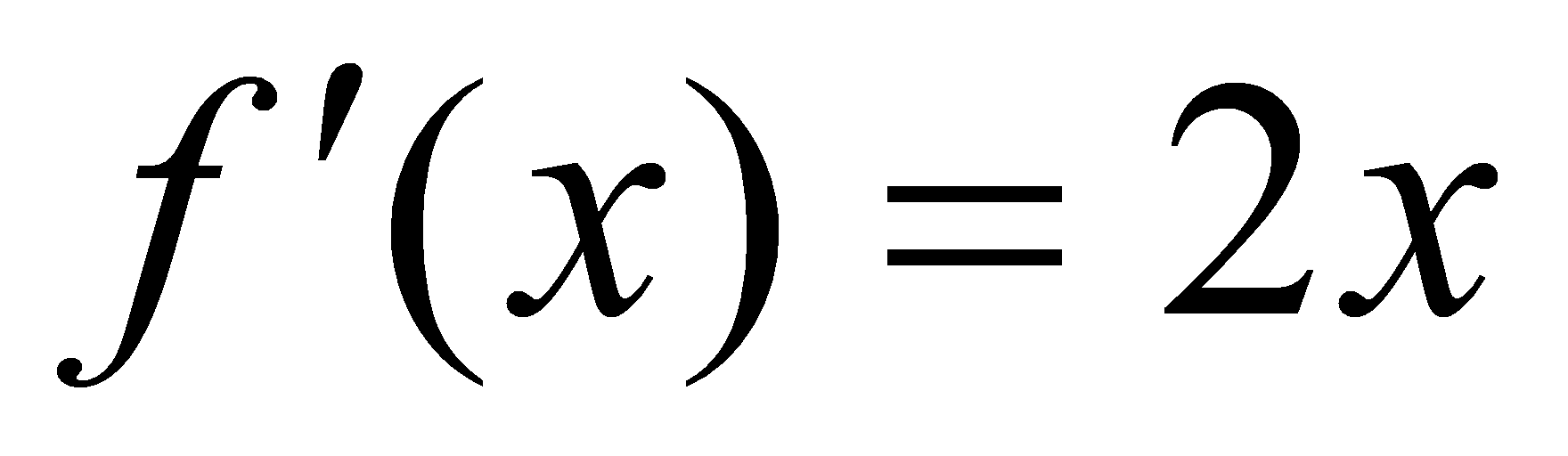 ,故
,故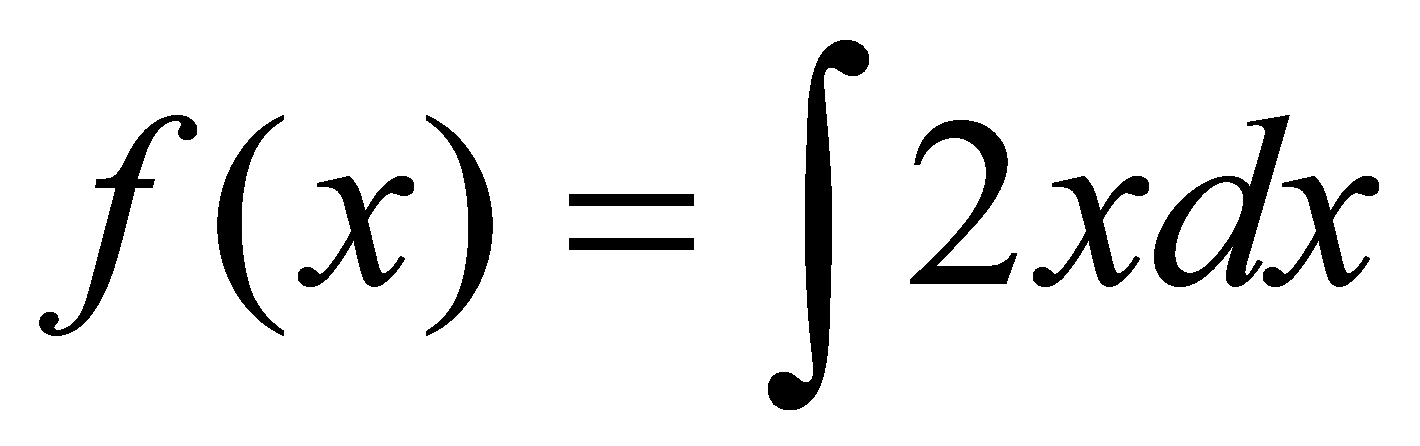 ,由于
,由于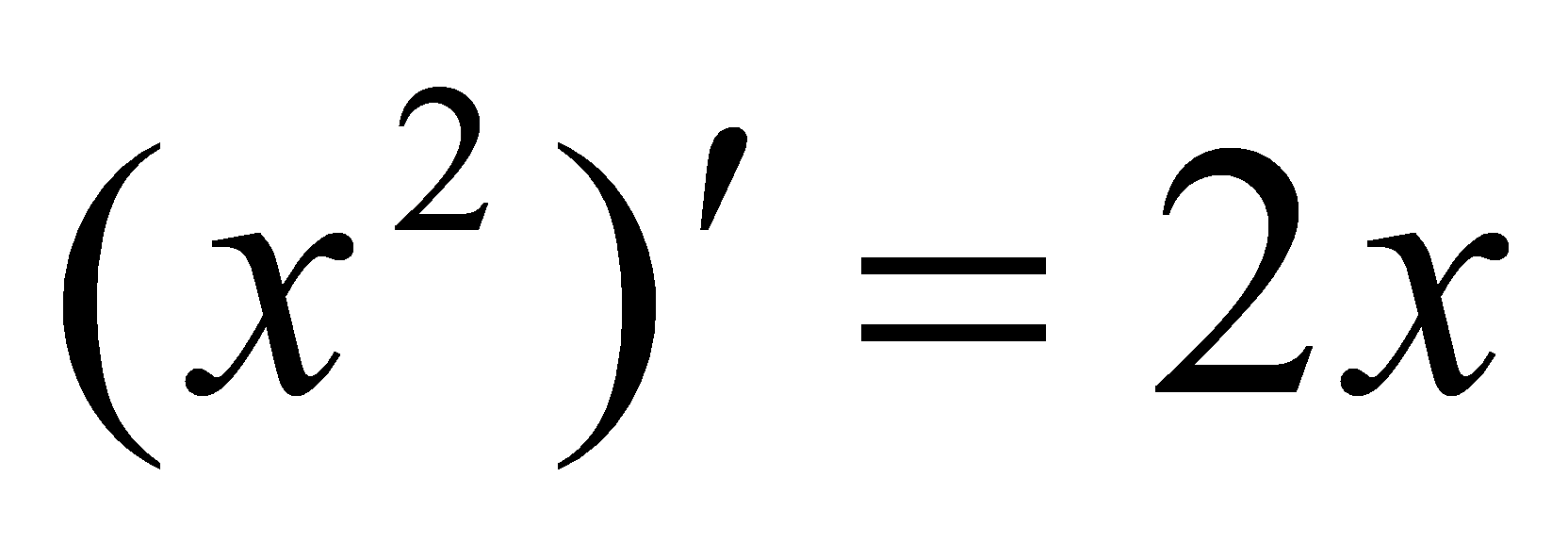 ,所以
,所以 ,又由于曲线满足
,又由于曲线满足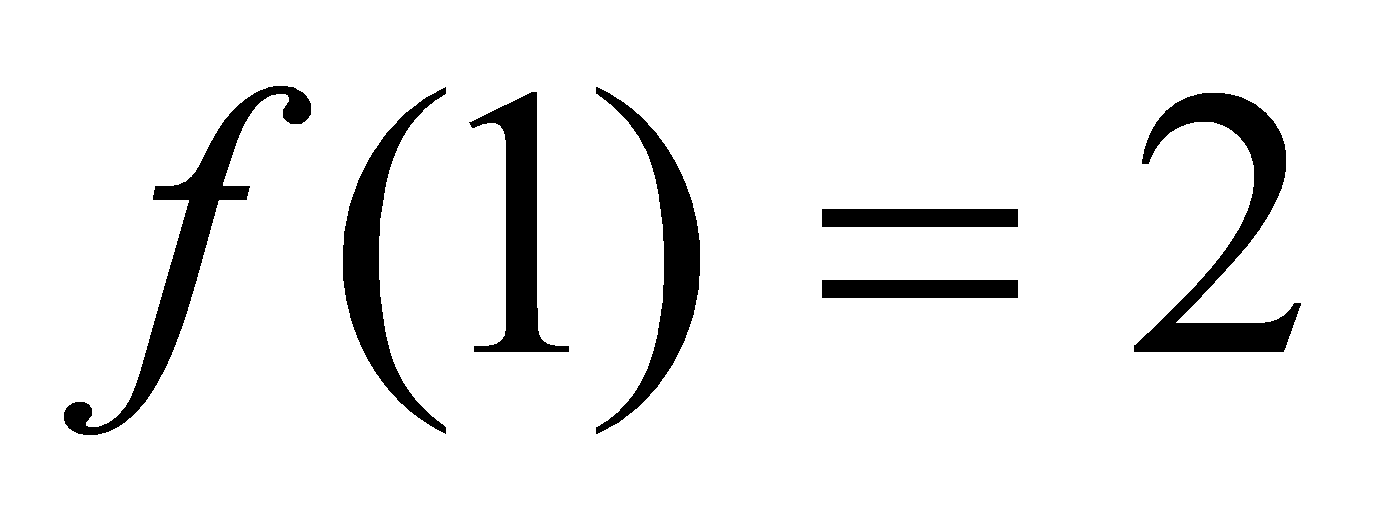 ,即有
,即有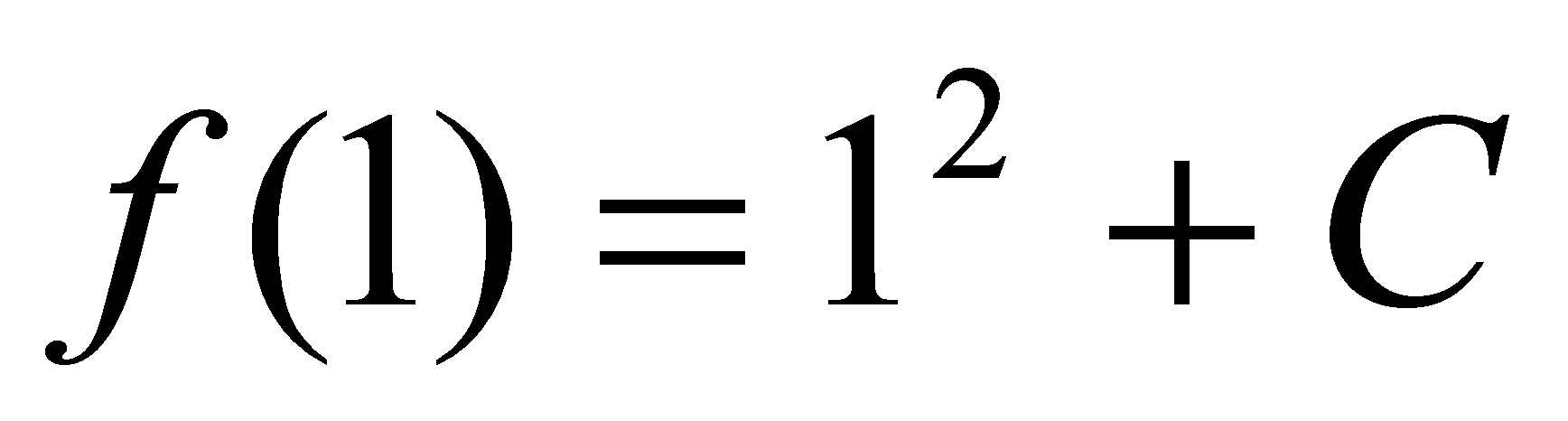 ,故
,故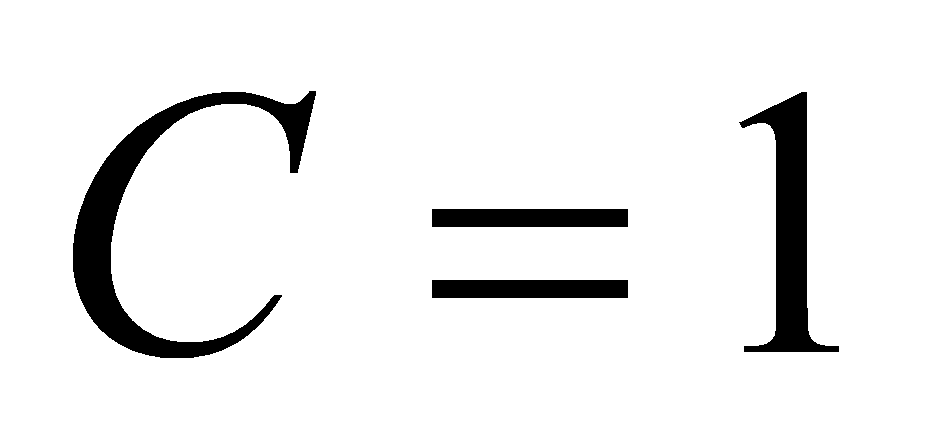 ,故所求的曲线方程为
,故所求的曲线方程为
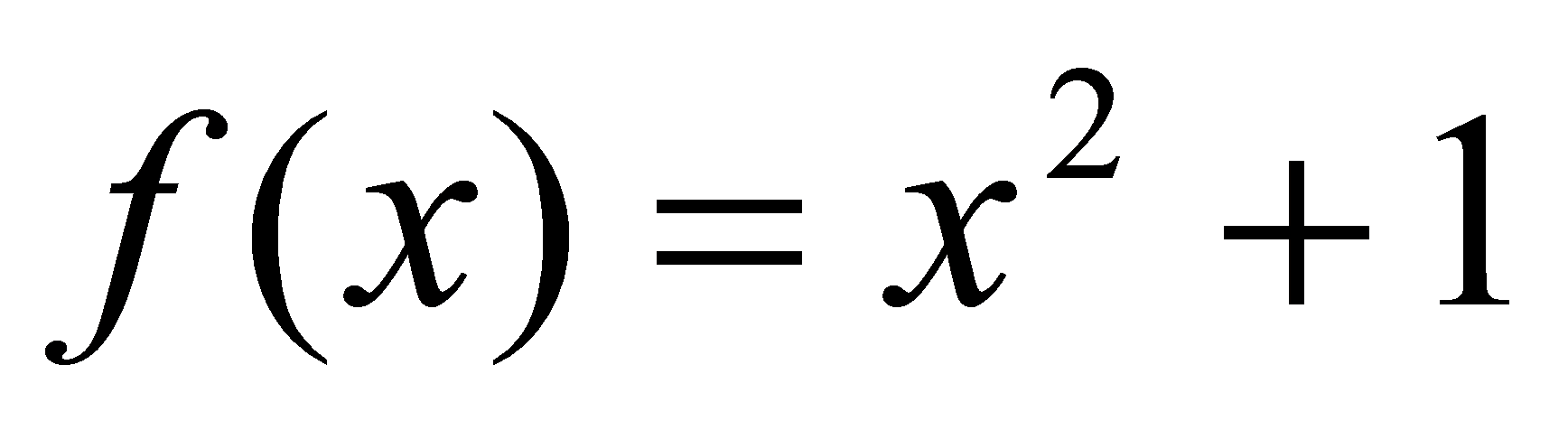 .
.
例4.1.2 因为,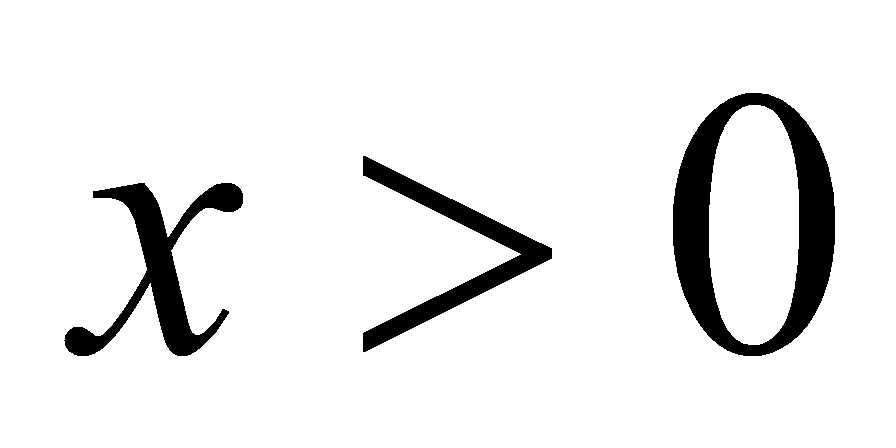 时,
时,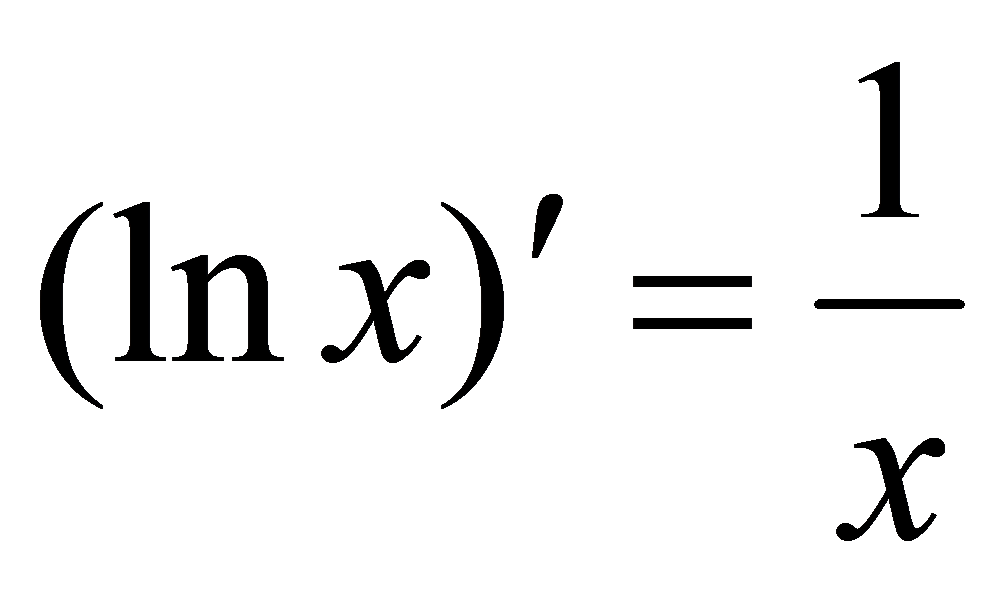 ;
;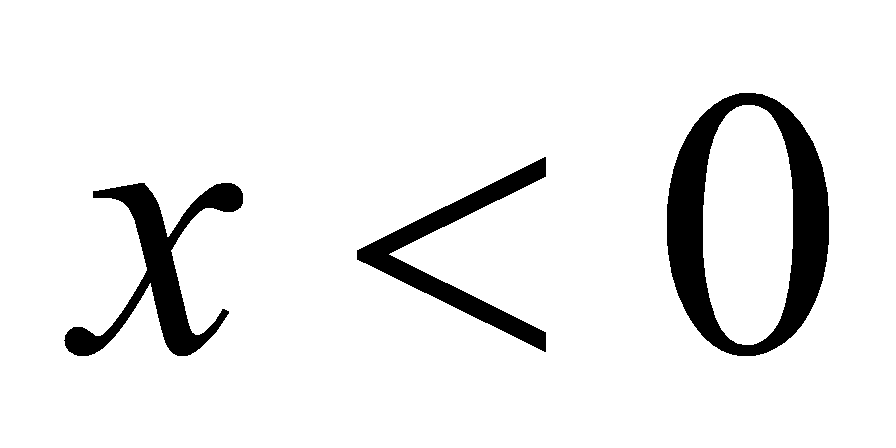 时,
时,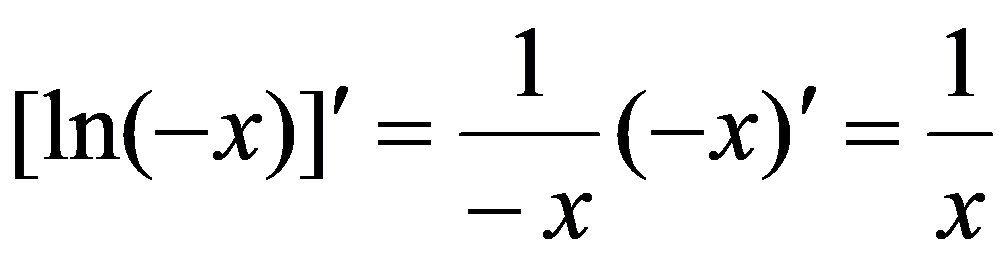 ,得
,得
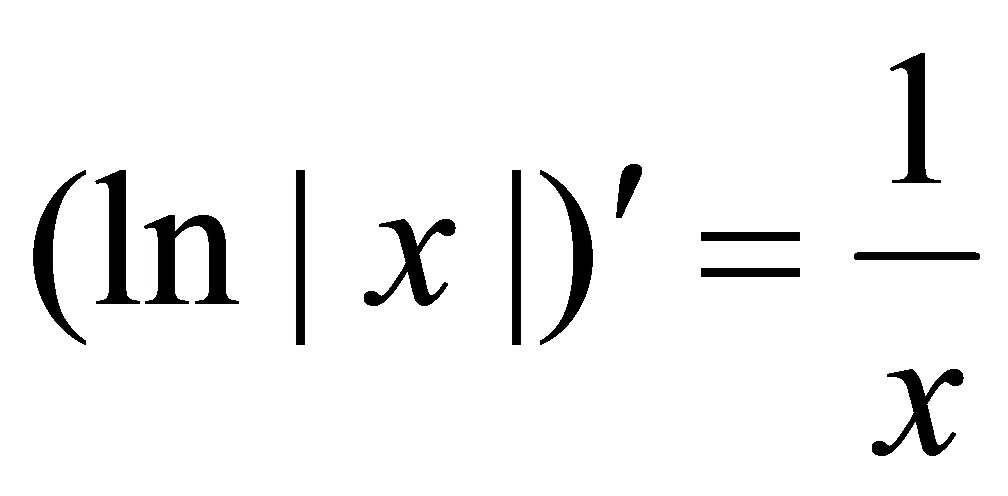 ,因此有
,因此有