5.3.2 定积分的分部积分法

定理5.3.2 设函数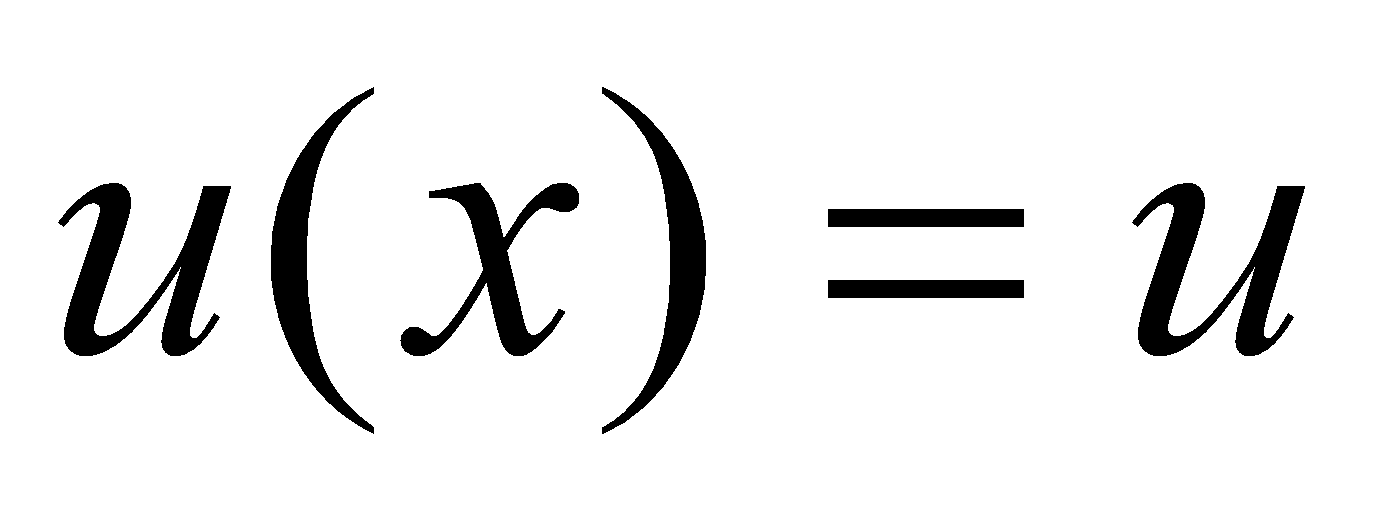、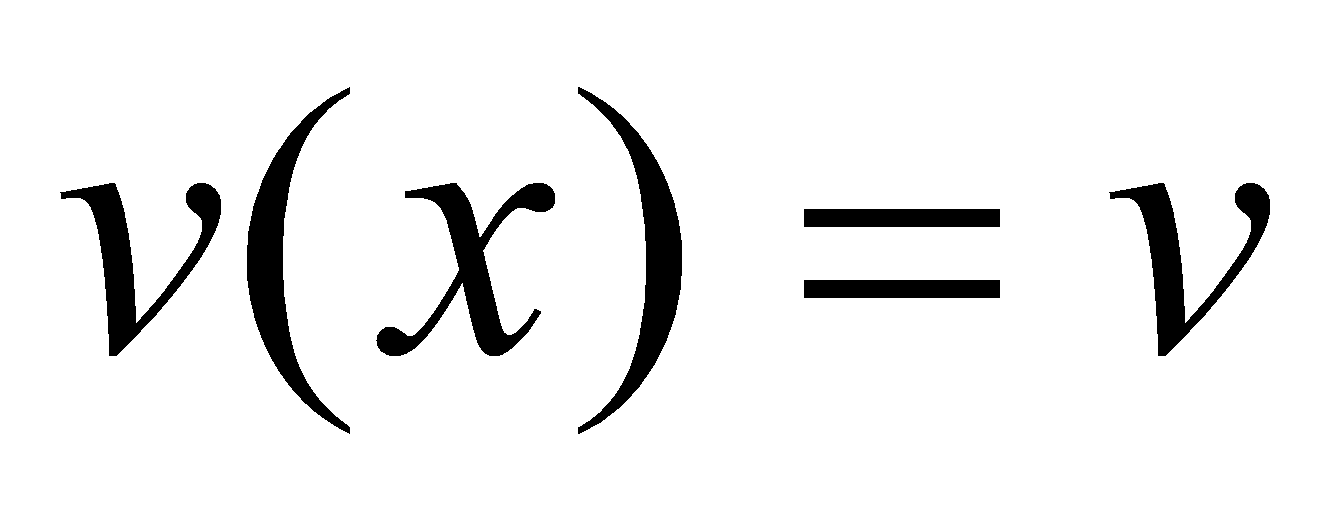在区间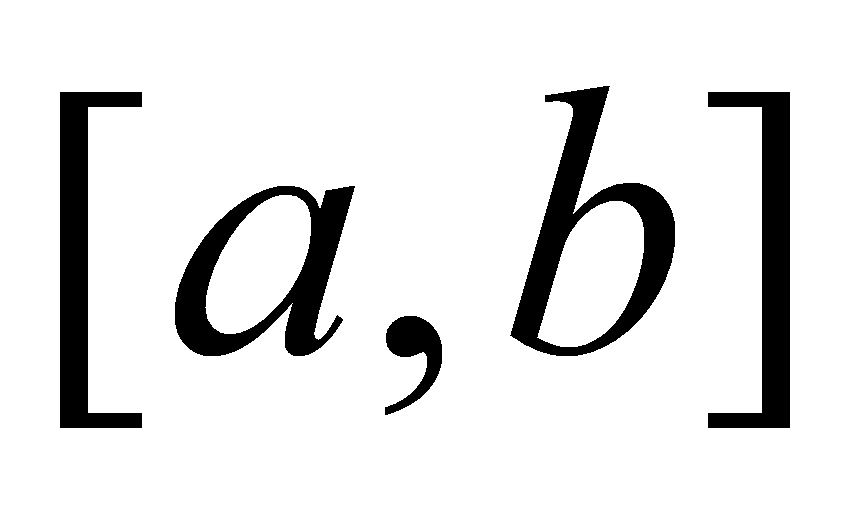上具有连续导数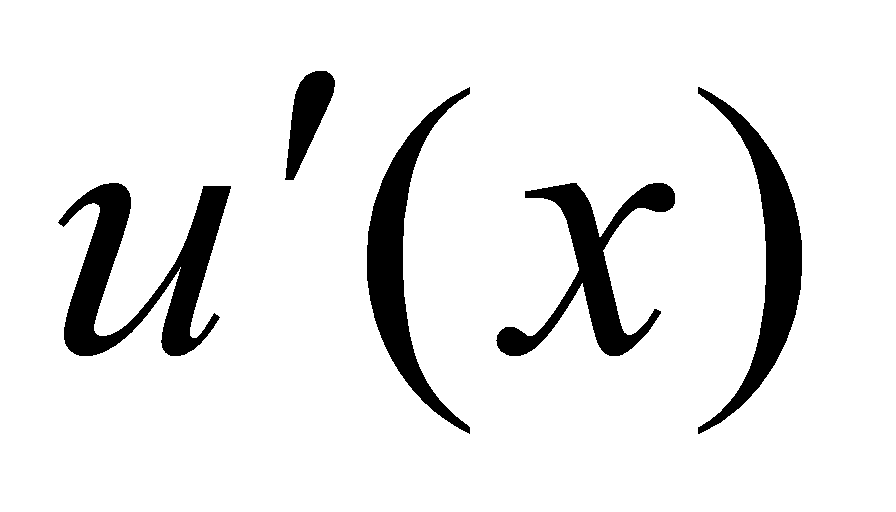、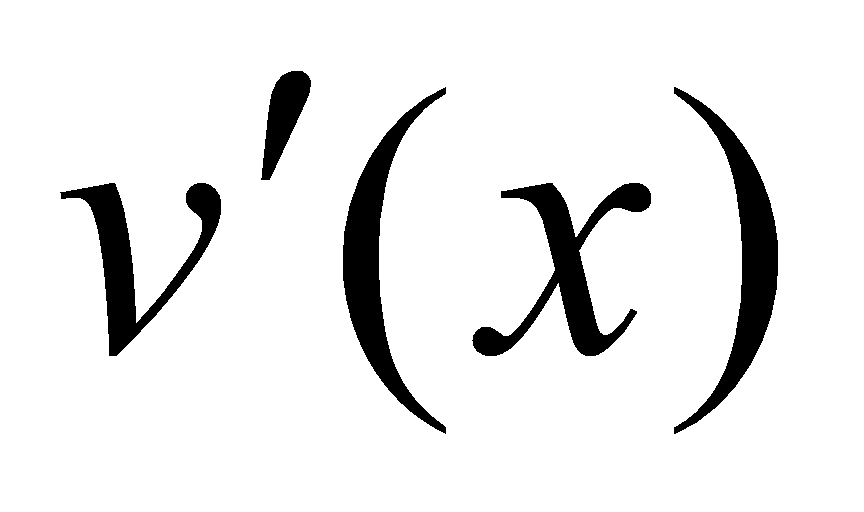，由于

，

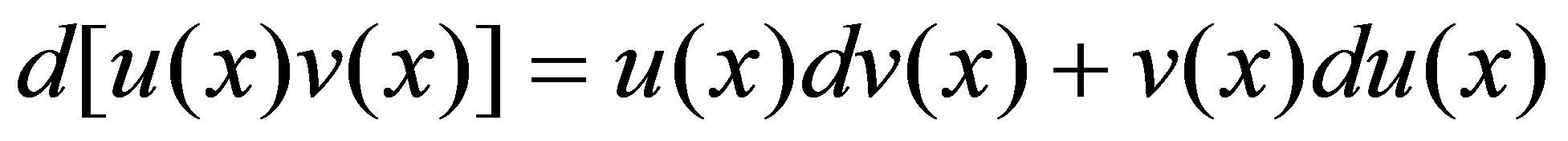则 ，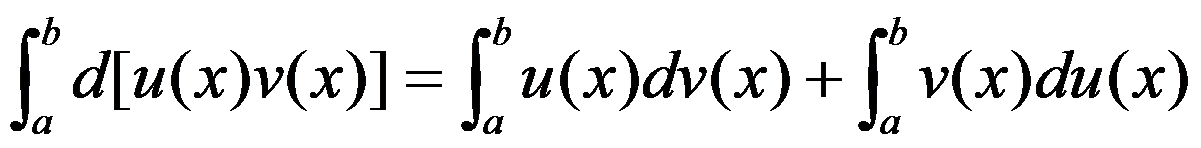

即

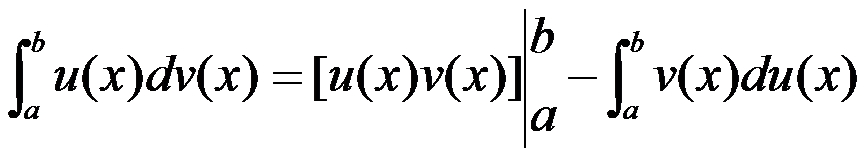
简记作 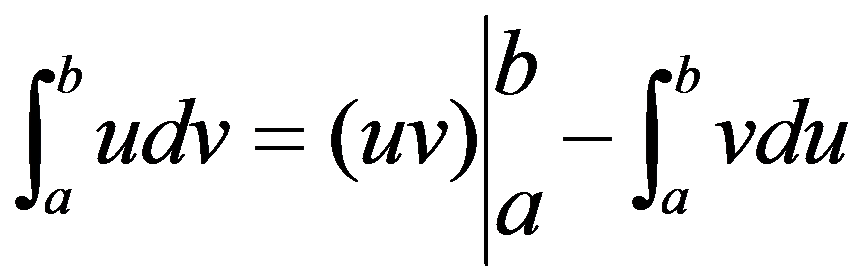（5.3.2）

这就是定积分的分部积分公式。此公式和不定积分的分部积分公式相似，只是每一项都带有积分限，其简便之处在于把积分出来的部分代入积分上、下限，变为具体的数值。

例5.3.8 计算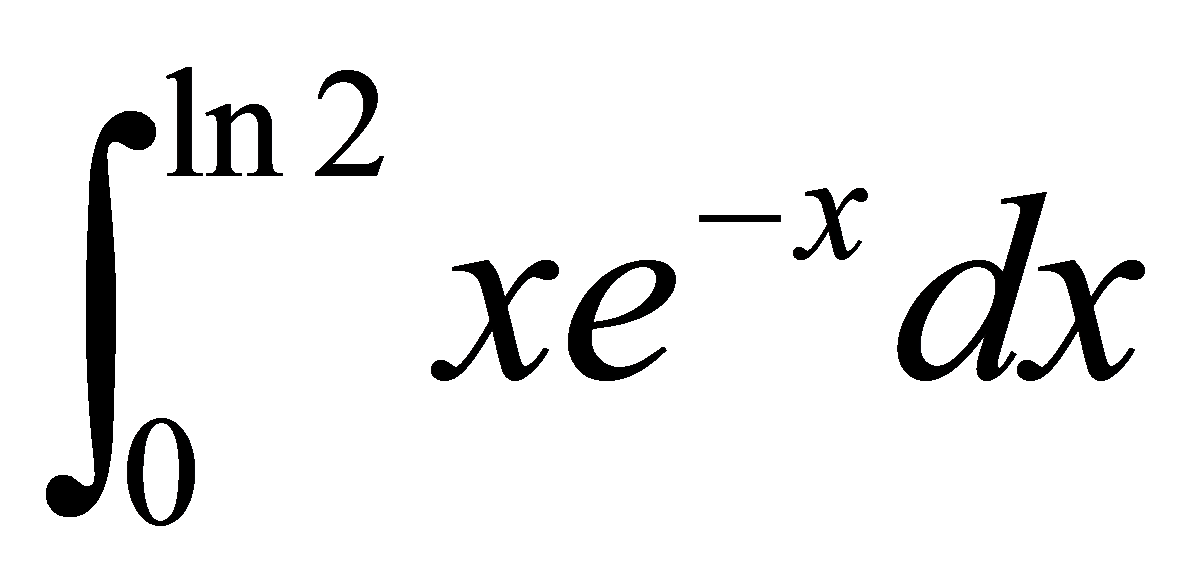

解 设 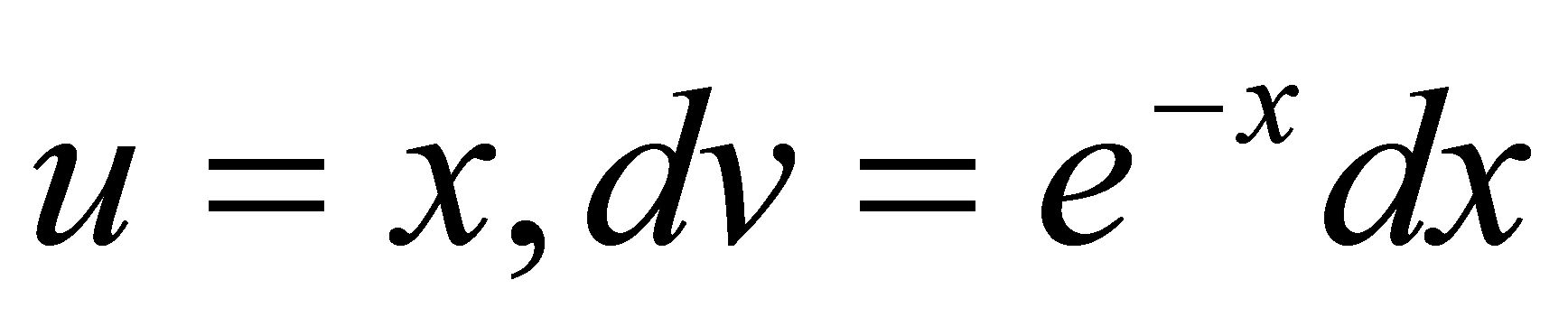， 则

， ，

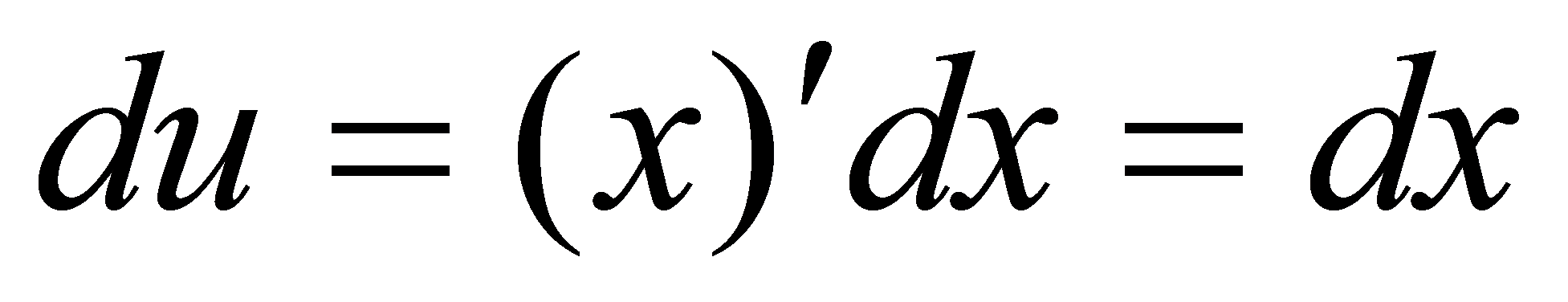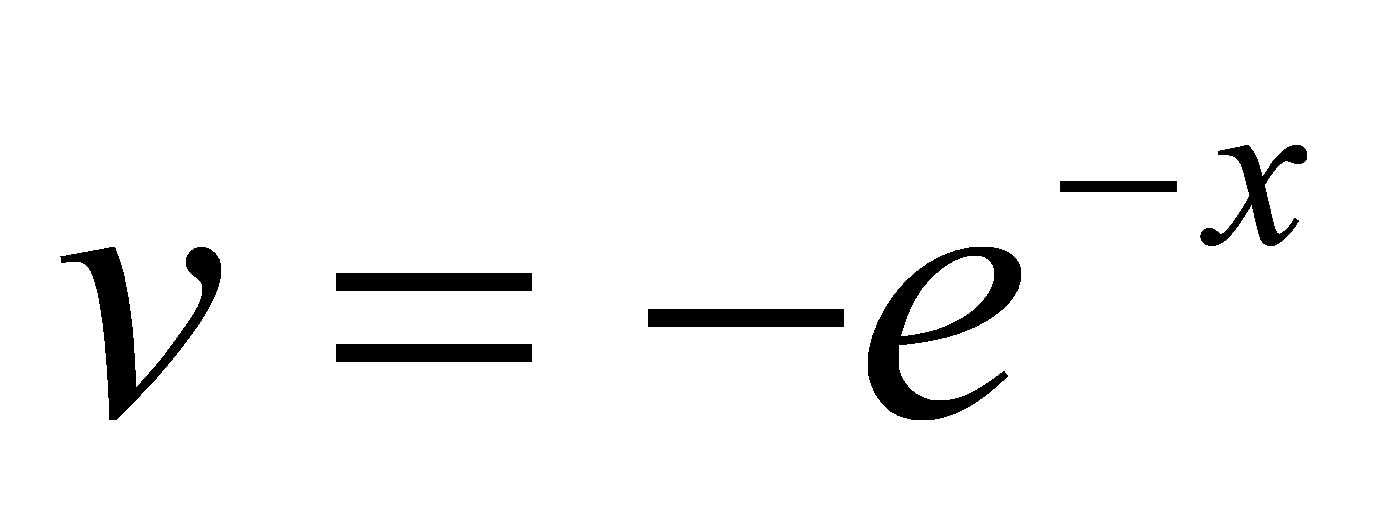于是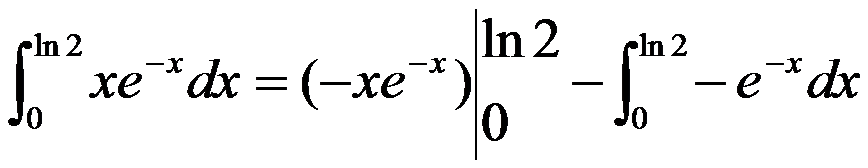

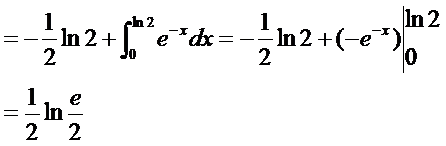
例5.3.9 计算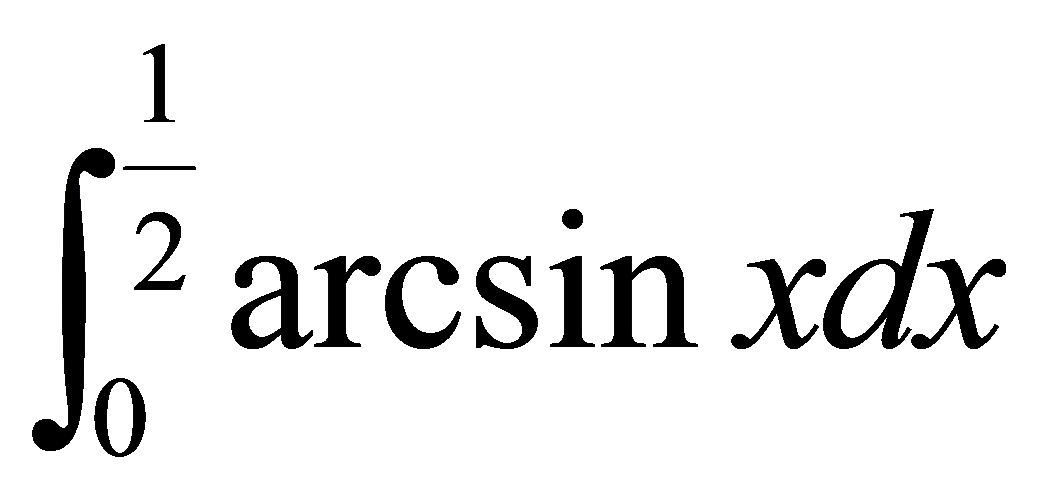

解 设 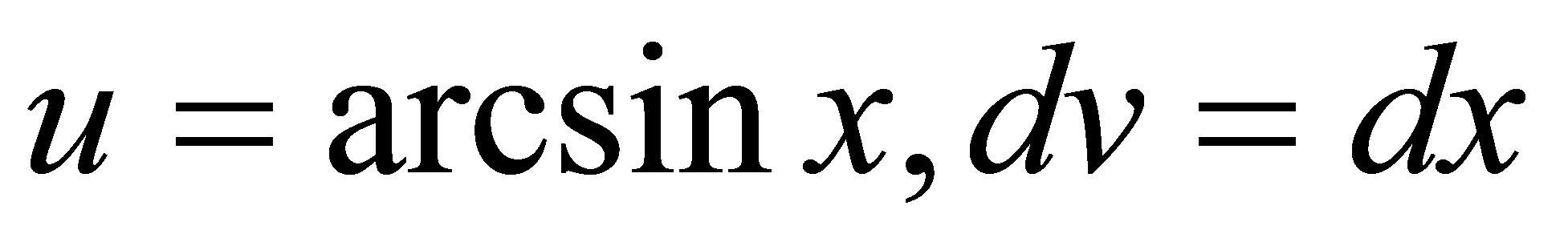， 则

， ，

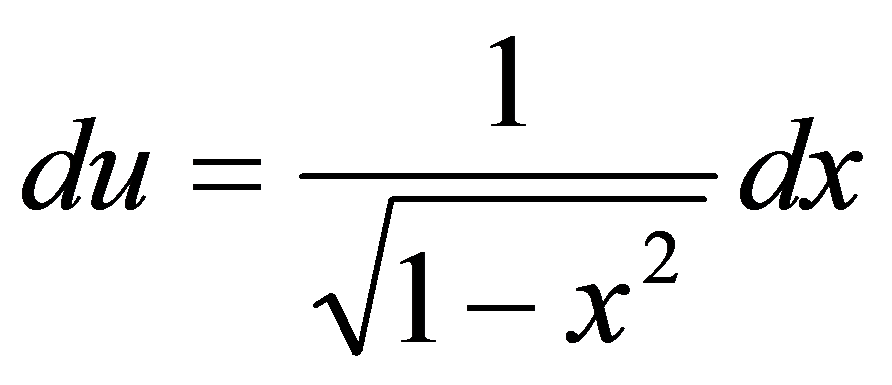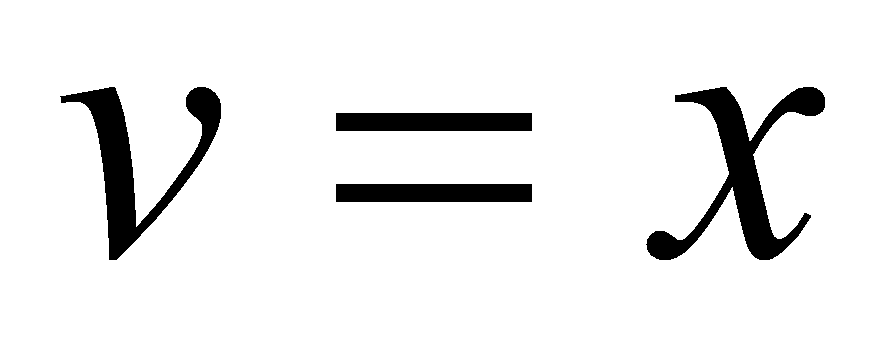于是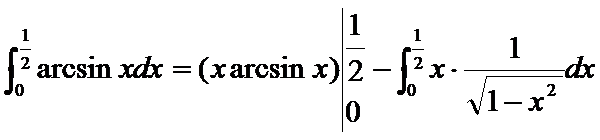

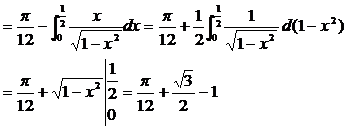
如果对计算已比较熟悉，也可不必写出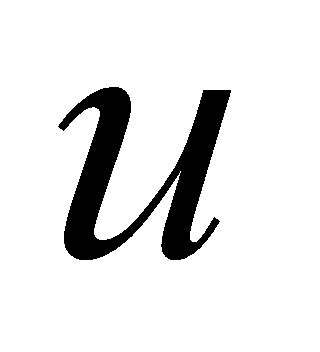、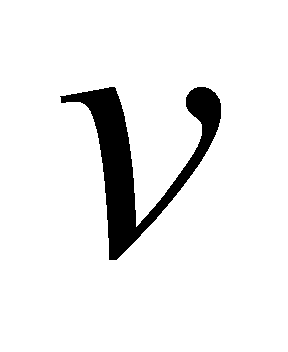，而直接应用分部积分公式。

例5.3.10 计算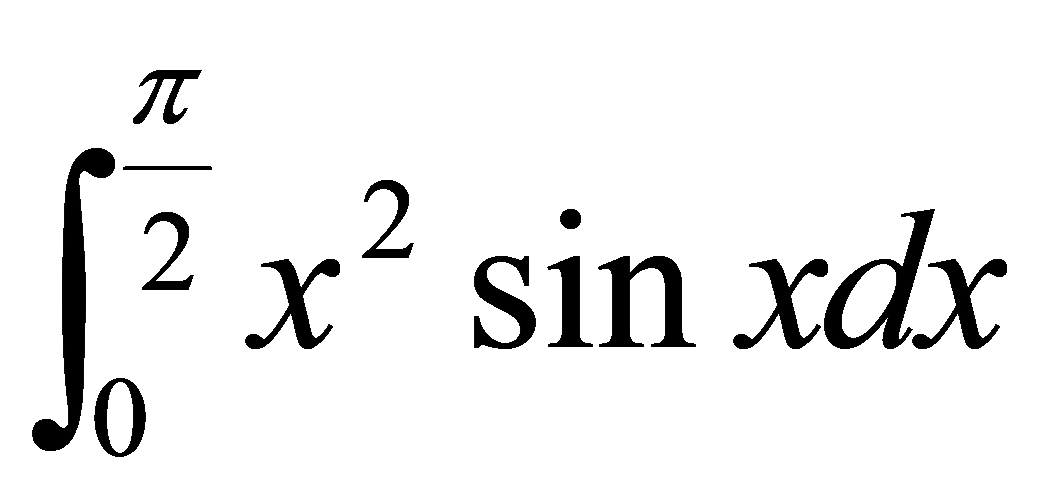

解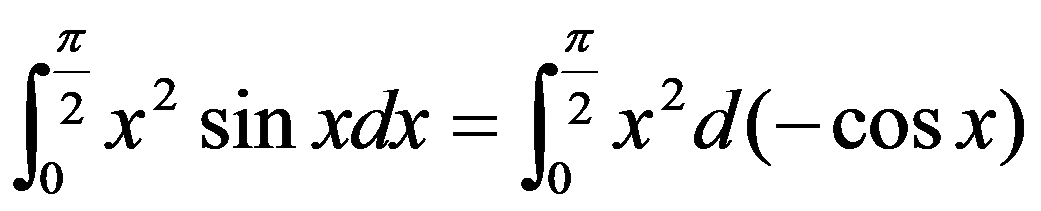

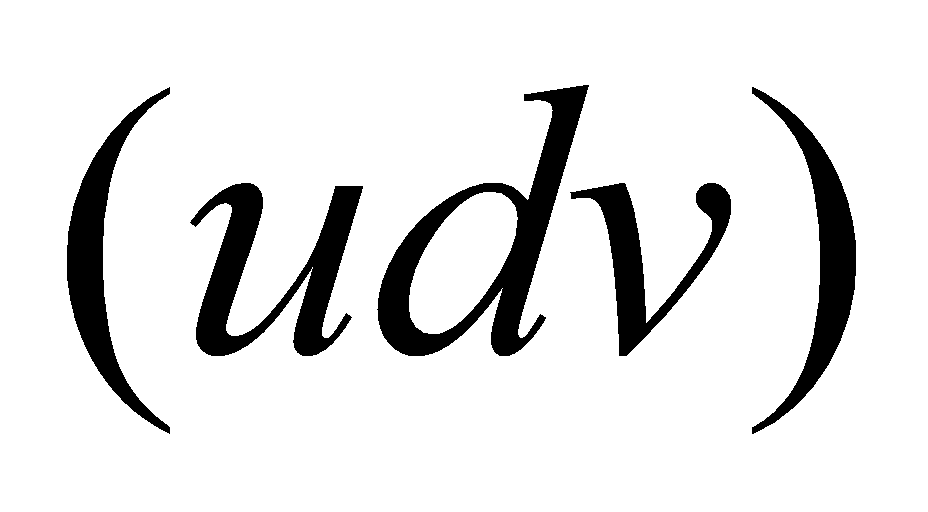
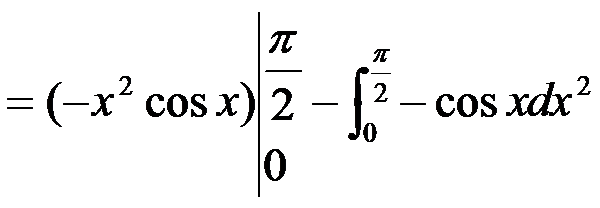
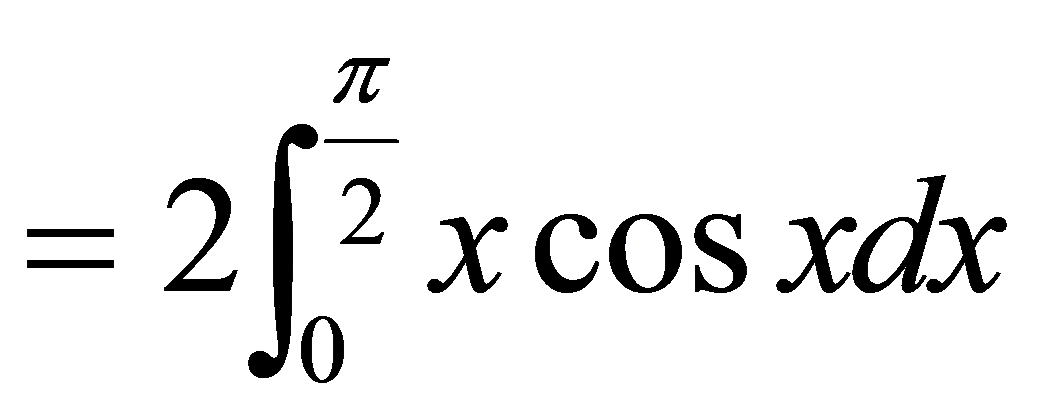
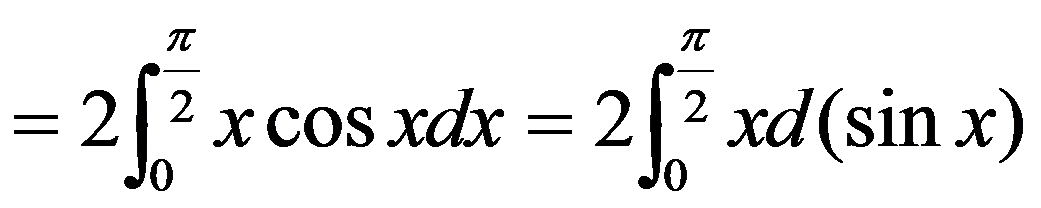
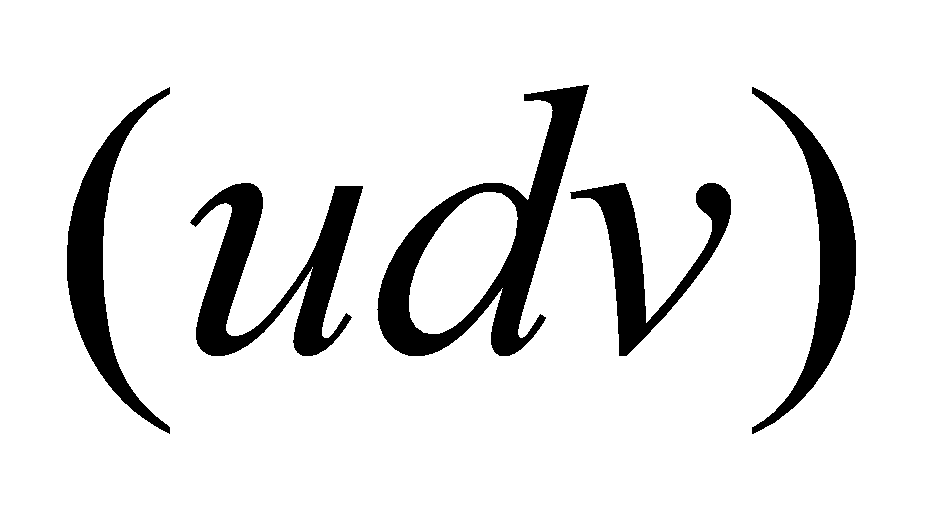
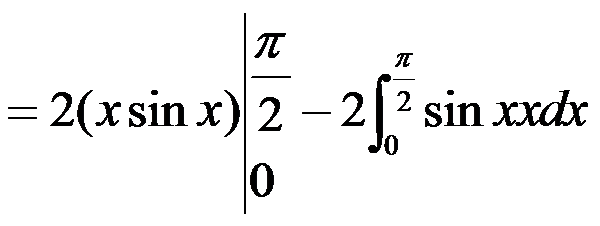
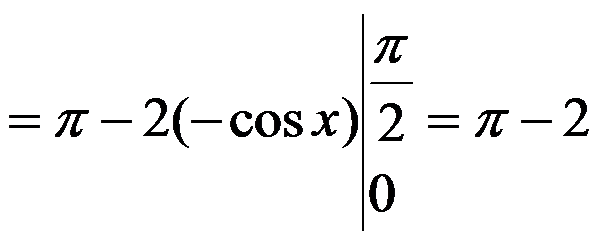
例5.3.11 计算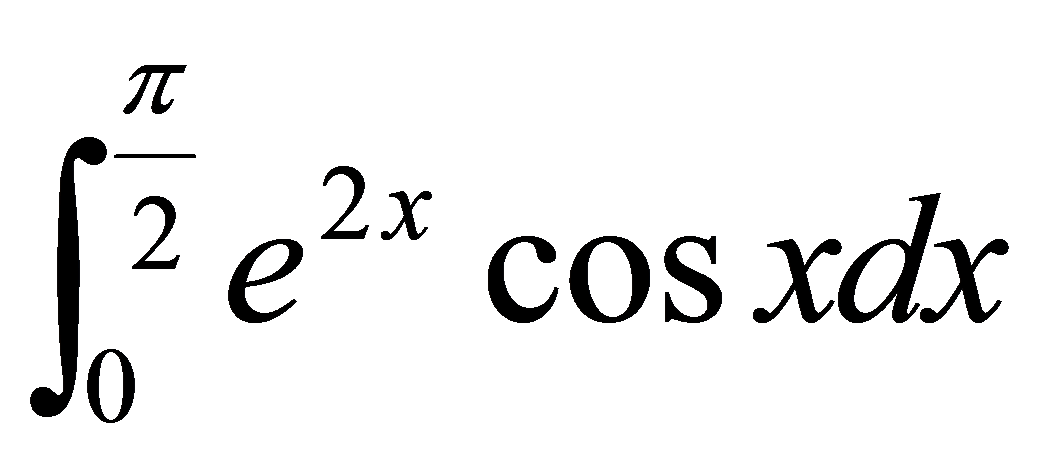

解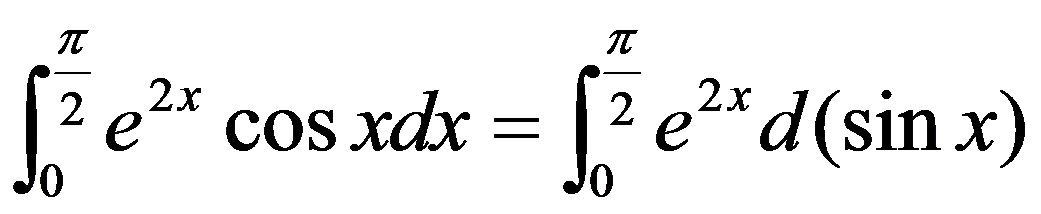

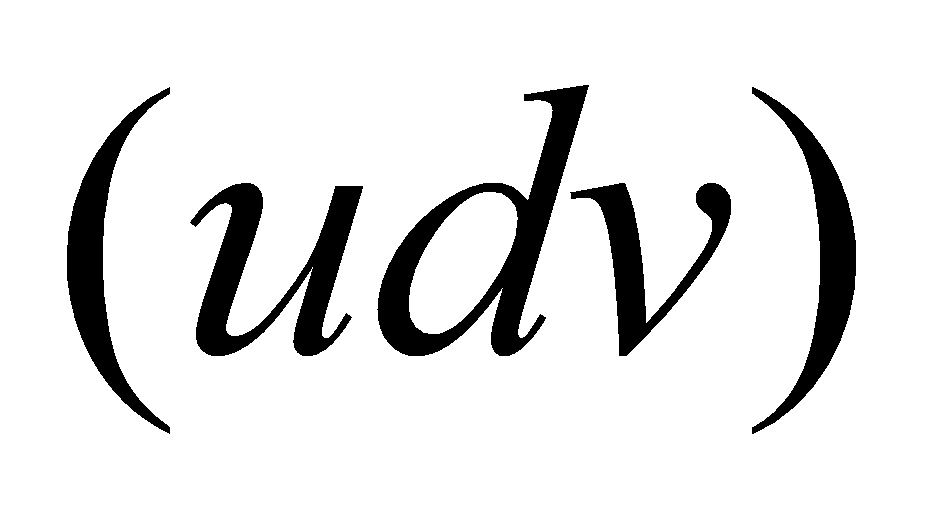
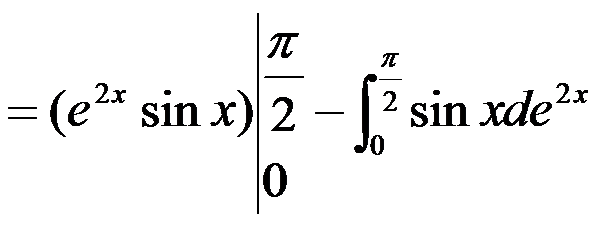
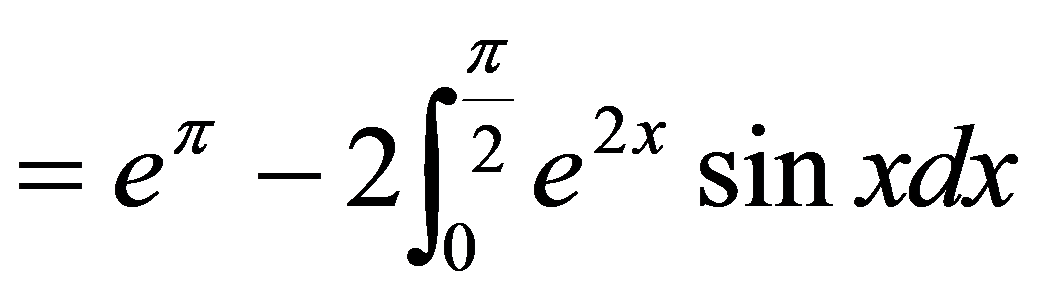
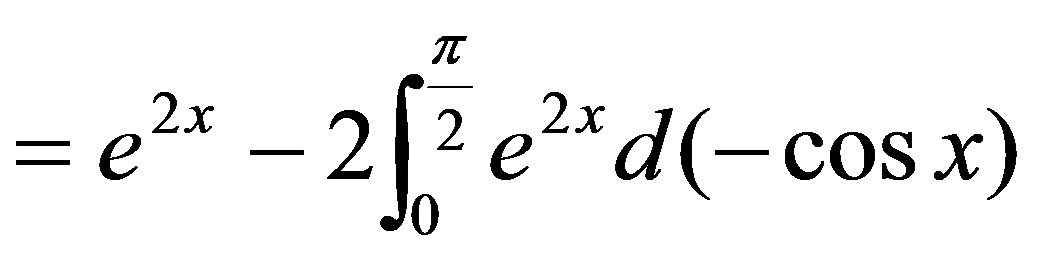
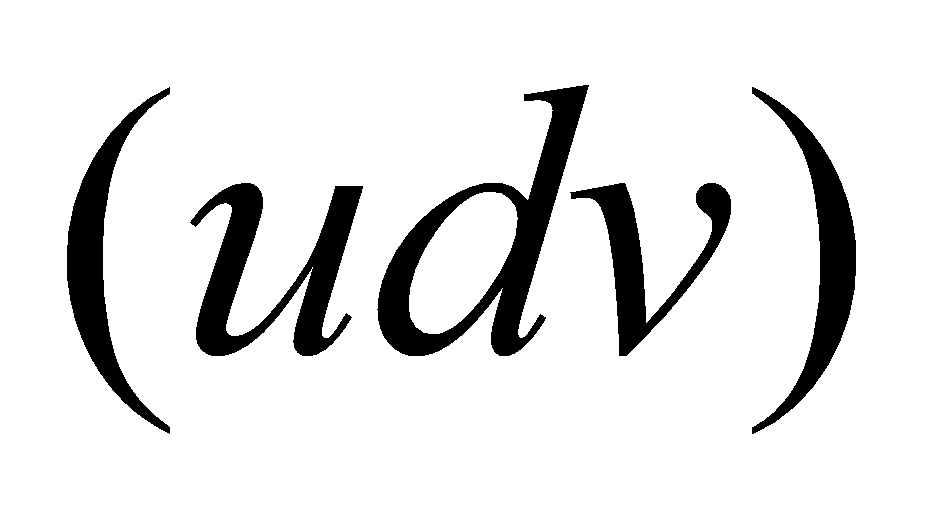
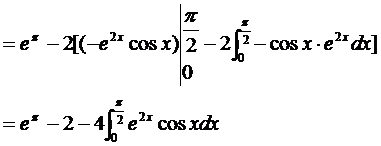
故 ，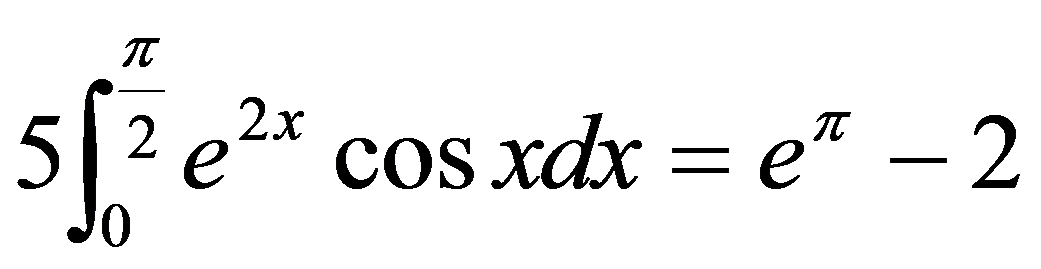

即 。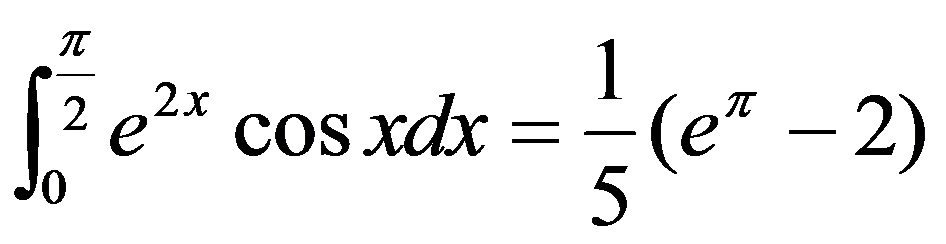

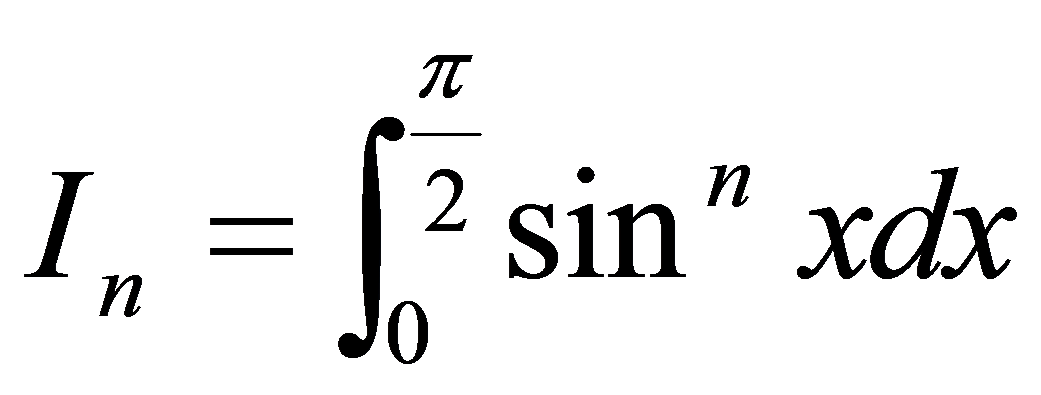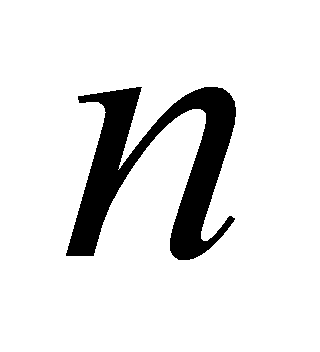例5.3.12 计算 （为自然数）。

解 由定积分的分部积分公式，可以证明：

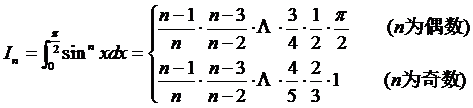
*5.3.3 定积分的近似计算

利用牛顿—莱布尼兹公式可以求部分函数的定积分，但实际应用中，经常遇到下列情况：

1）欲求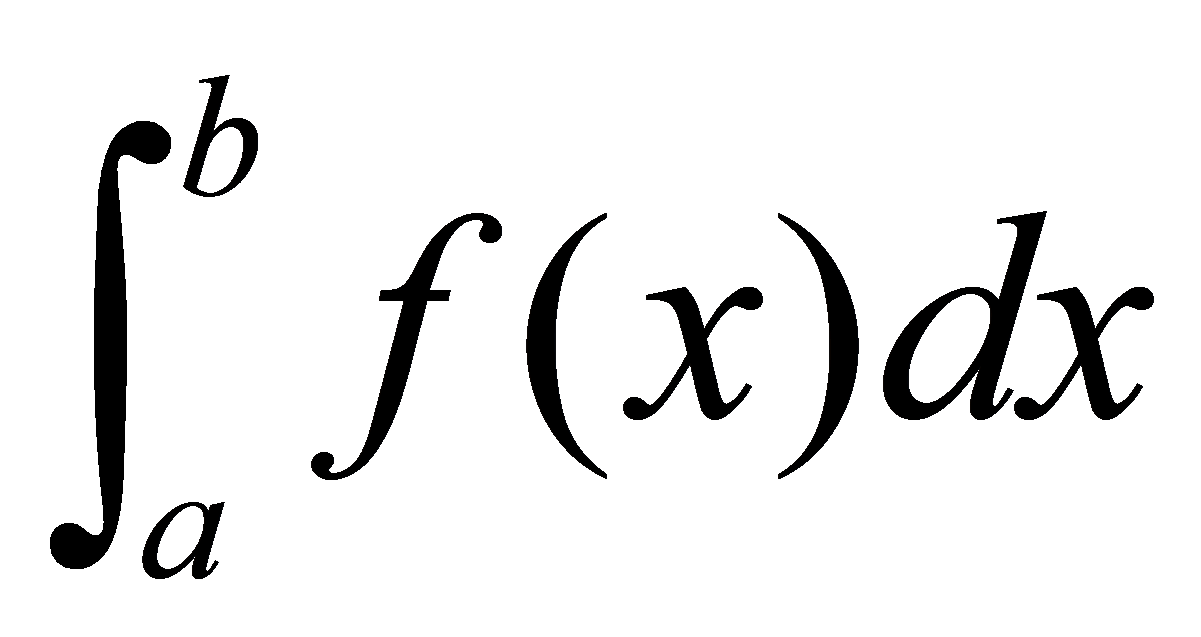的值，而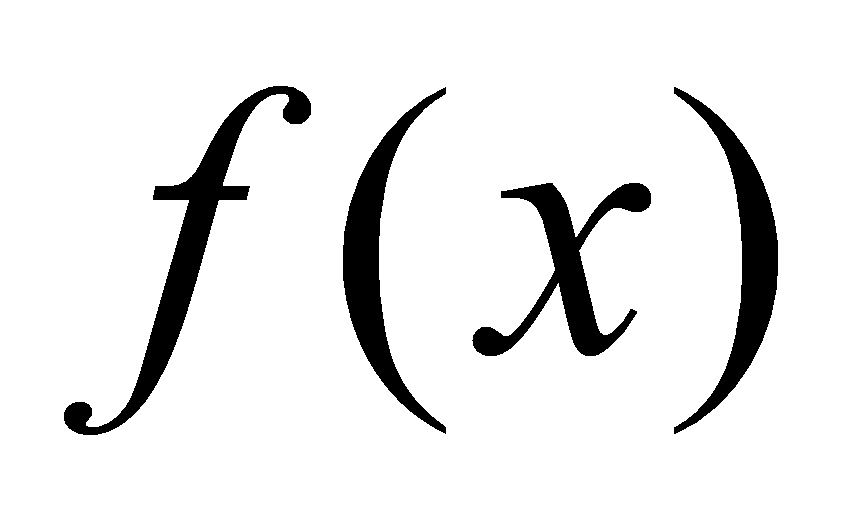的原函数根本不能用普通的初等函数表示出来，如、。

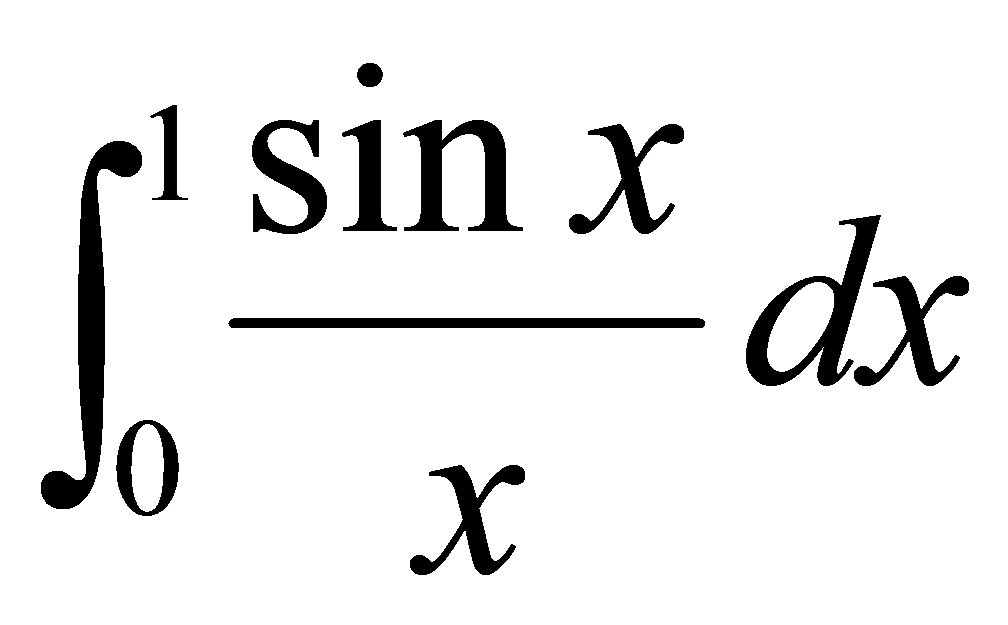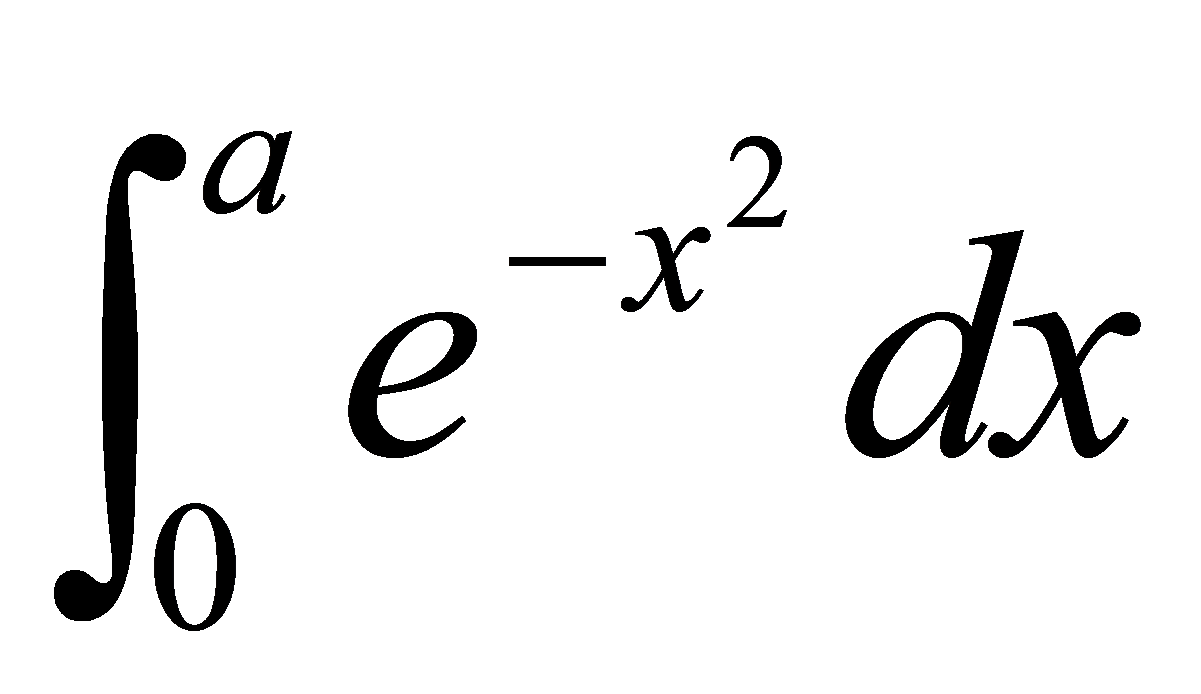2）若被积函数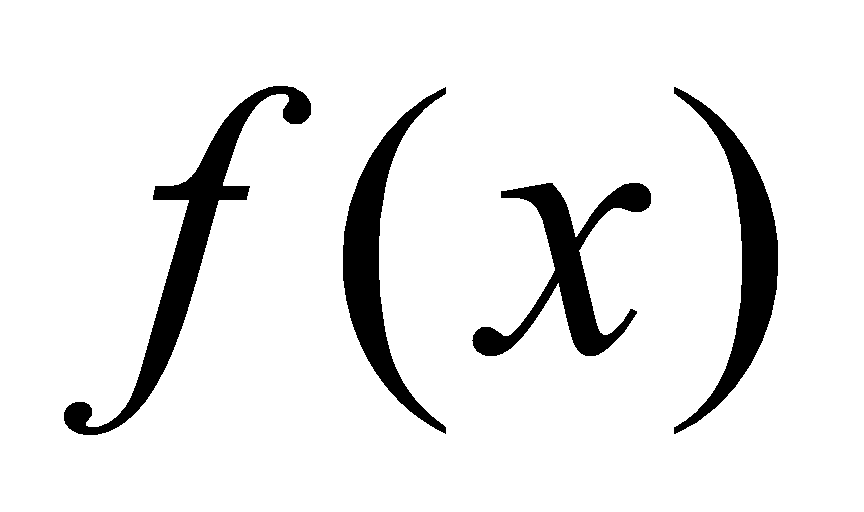是用表格方式表示的，则无法求出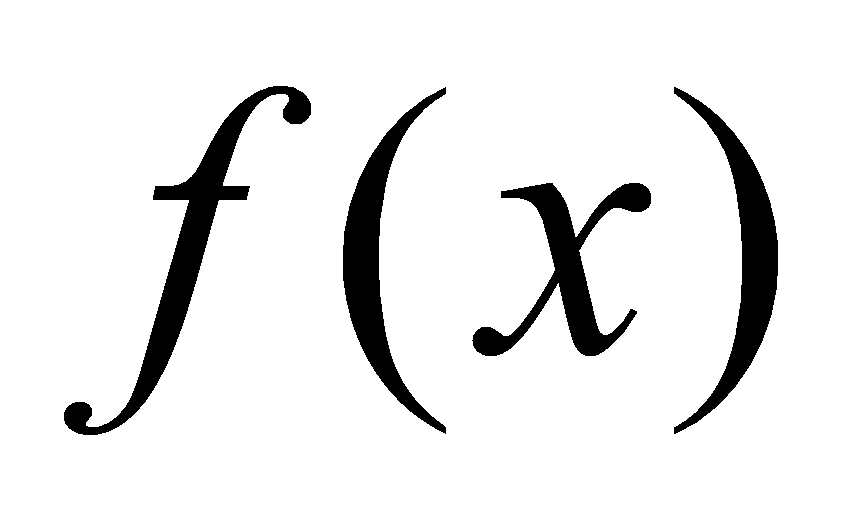的原函数。

3）有时从理论上可以证明被积函数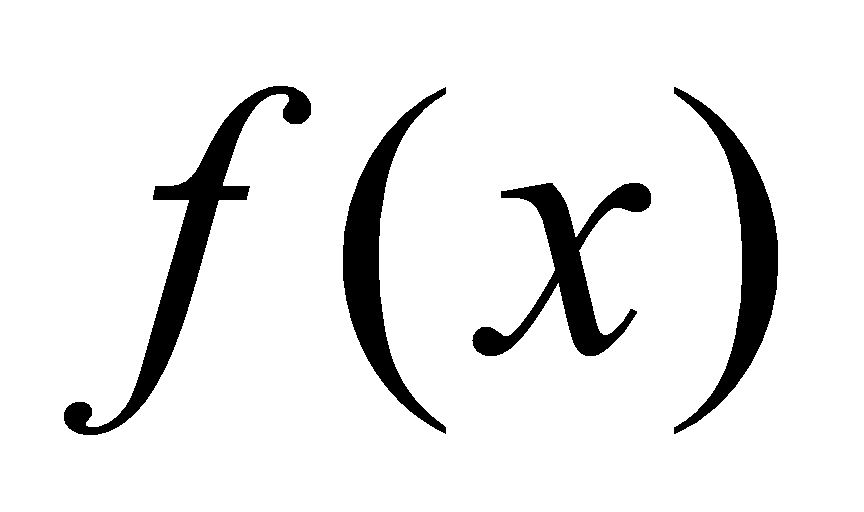的原函数可以用初等函数表示出来，但计算过程相当复杂，即便能够求出来，得到的积分值也有可能是近似值。

所以定积分的近似计算已经成为应用定积分解决实际问题时不可缺少的方法。

定积分的近似公式的基本思想是，从求面积的近似值着手，导出相应的求定积分的近似公式。这里只介绍几种简单而又比较有效的方法。

（1）矩形法（rectangular method）

矩形法的基本思想是将曲边梯形分成若干个小曲边梯形，再用小矩形近似地代替小曲边梯形，然后将各小矩形面积累加，得定积分的近似值。

计算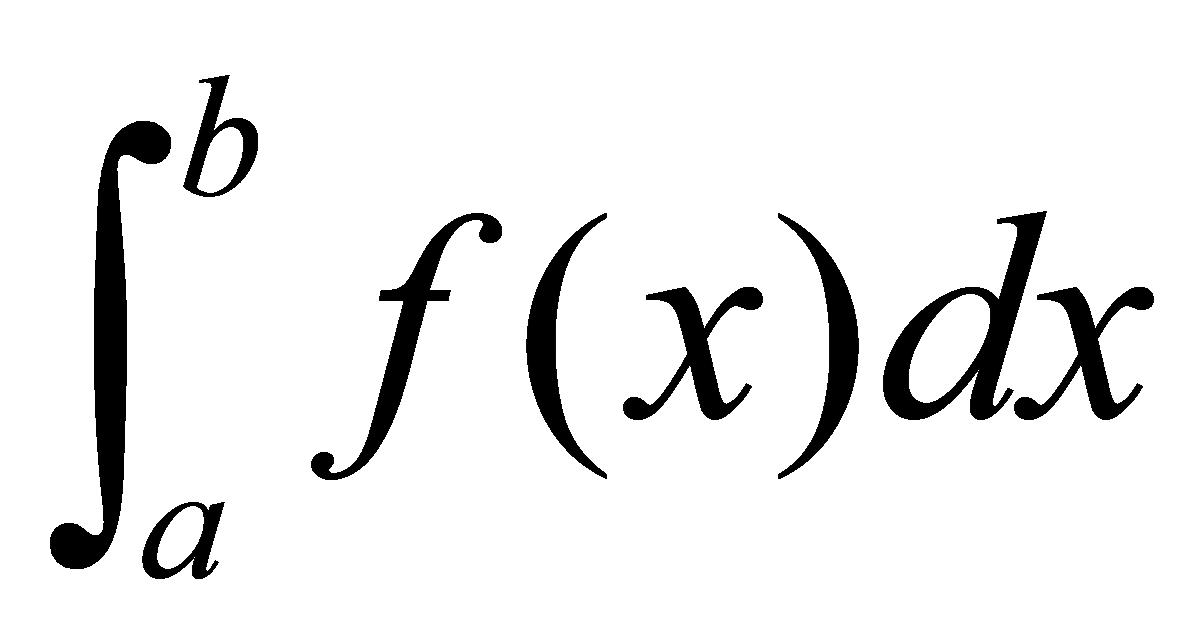，具体作法如下：

用分点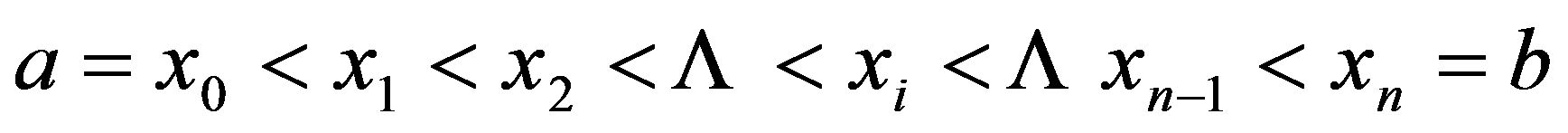把区间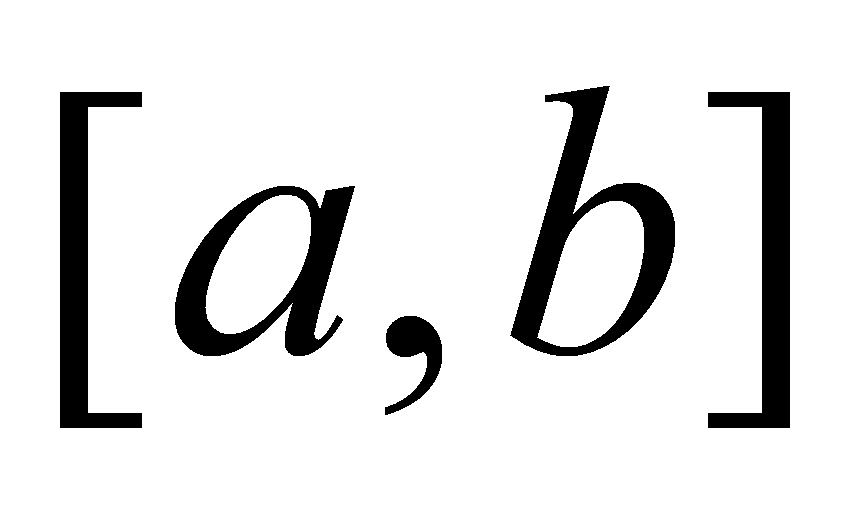分成n等分，每等分的长度为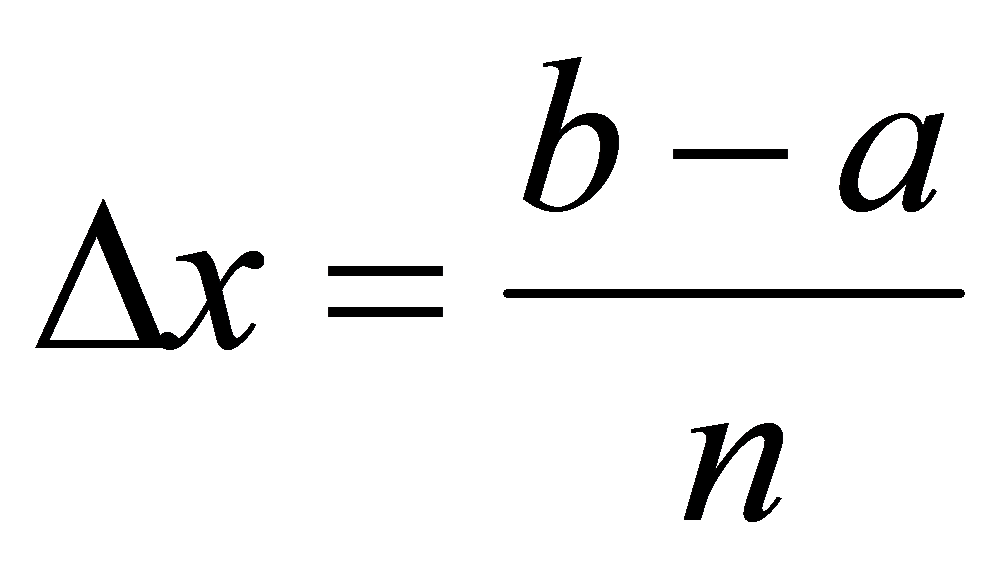，过各分点作平行于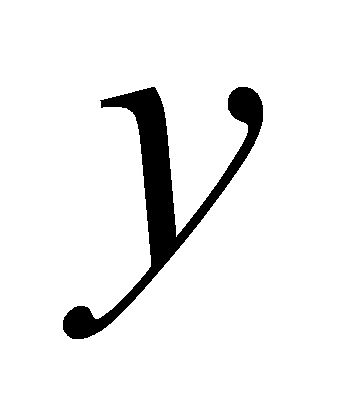轴的直线分别交曲线于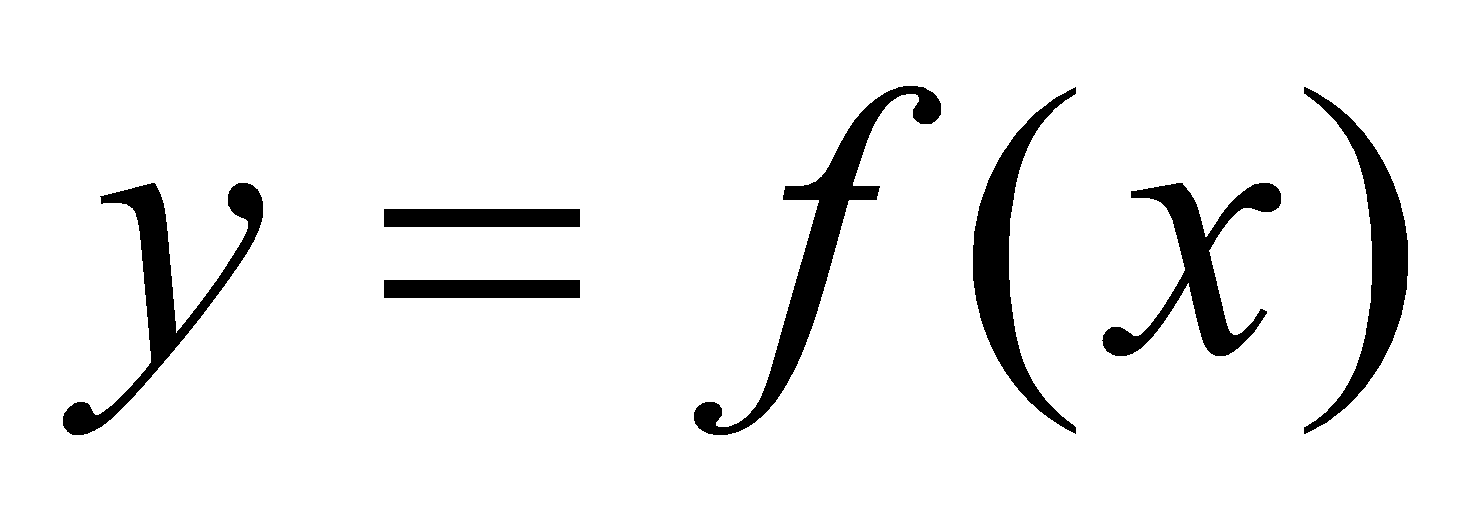，并得到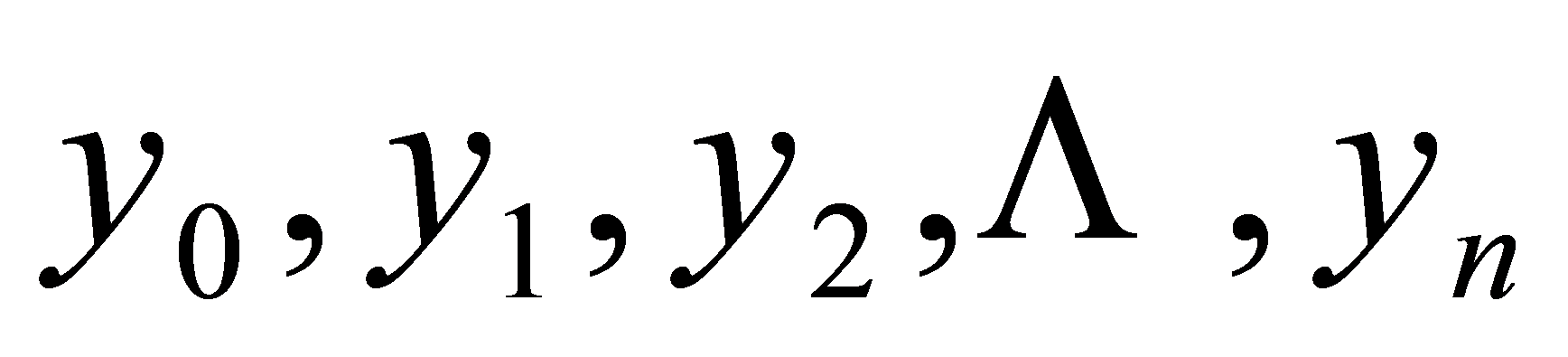，原来的图形被分成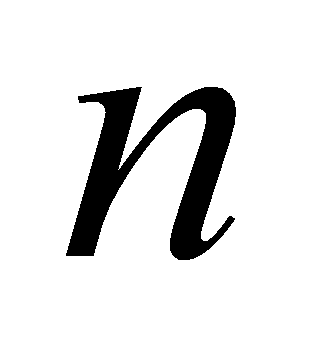个小曲边梯形，如图5-9。

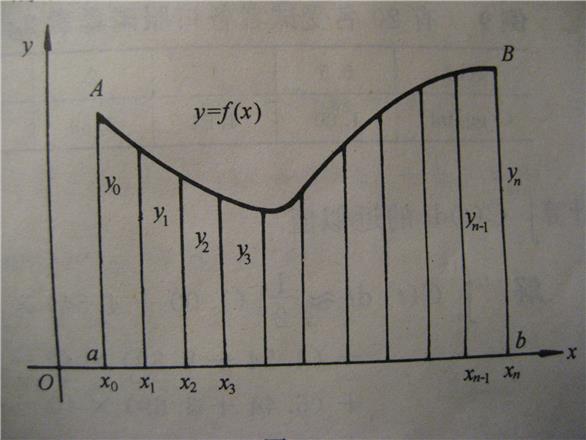
图5-9

每个小曲边梯形的面积都用相应的小矩形面积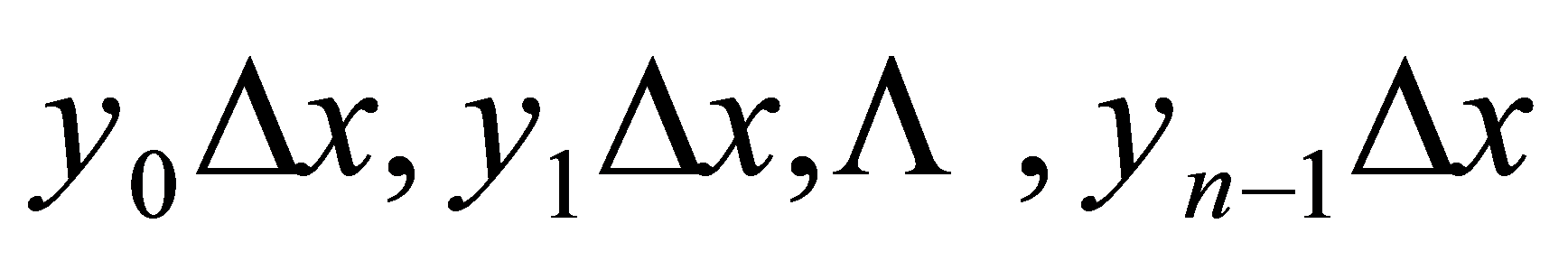或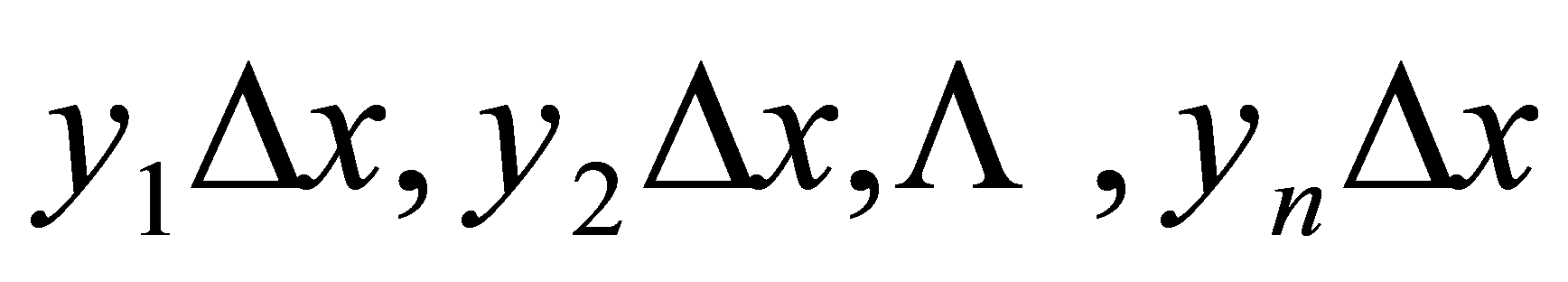来近似代替，把它们加起来，就得到

，

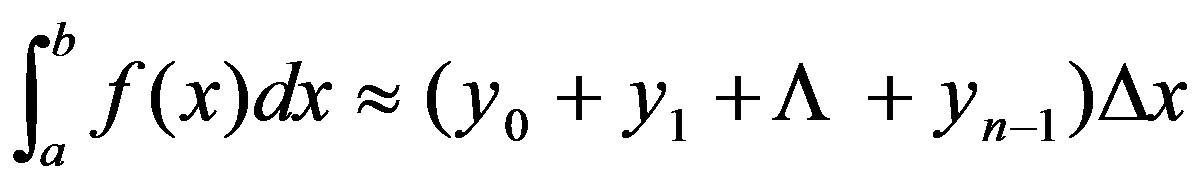
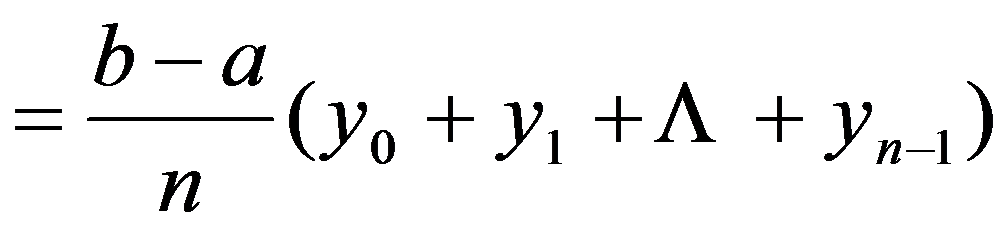或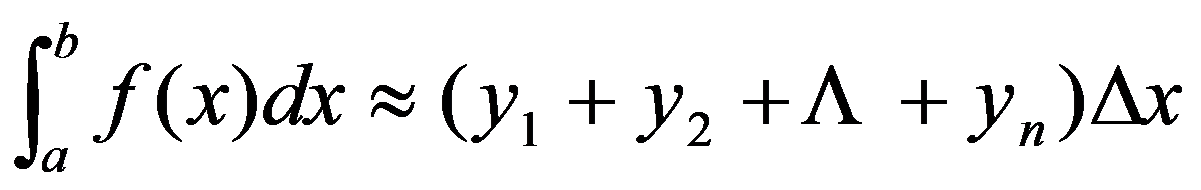

，

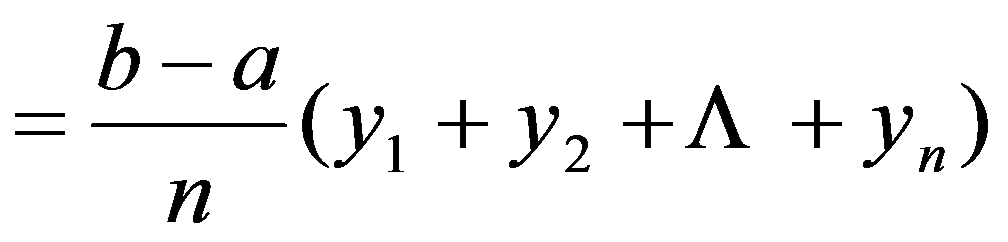这就是用矩形法计算定积分近似值的公式。

（2)梯形法（trapezoidal method）

用小梯形代替小曲边梯形来近似计算定积分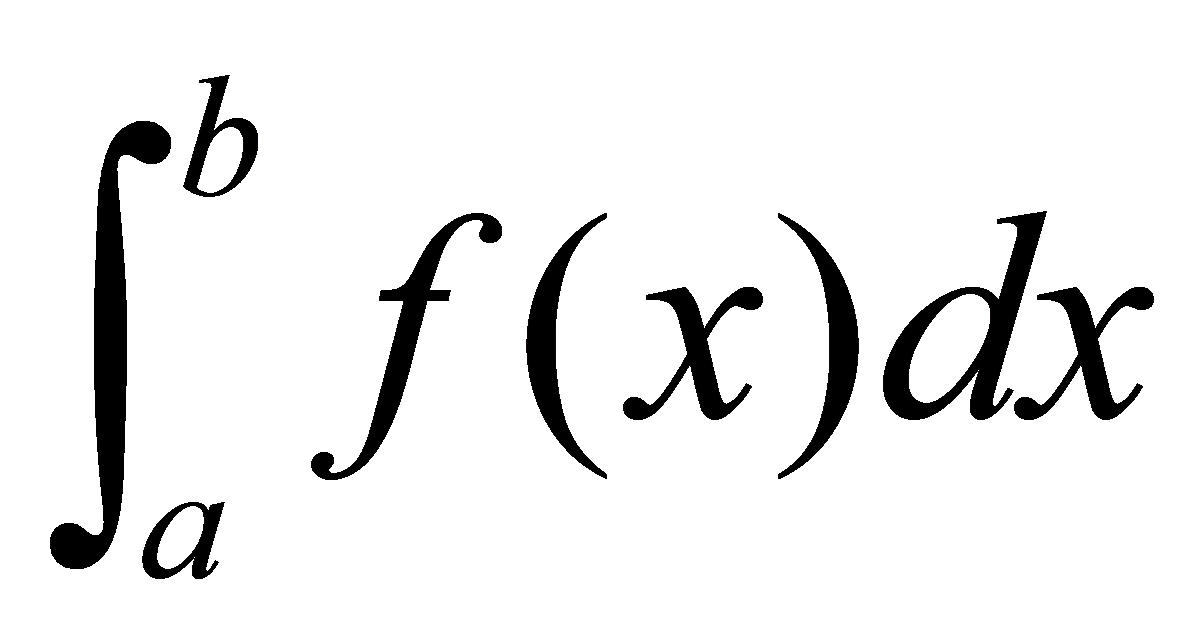的方法为梯形法。

把区间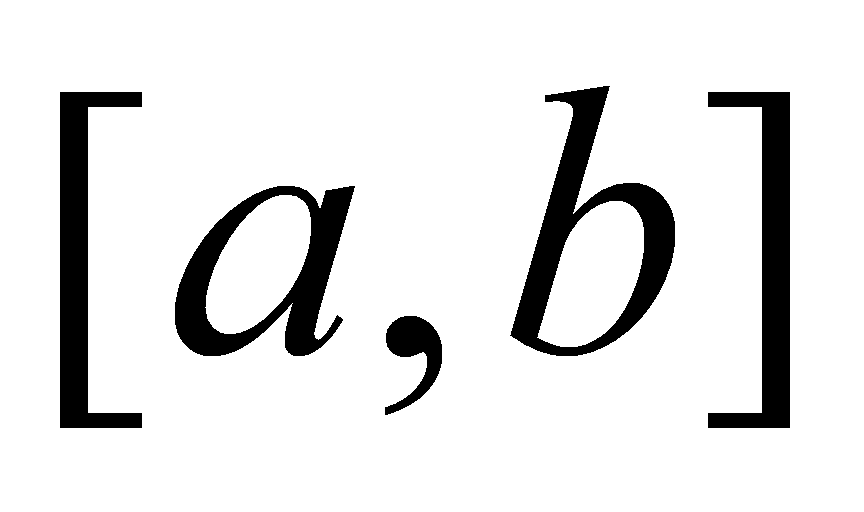用分点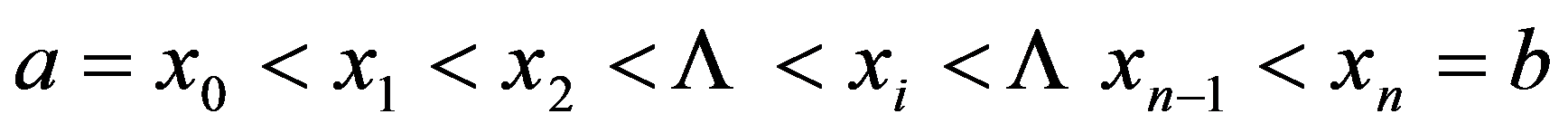分成n等分，每等分的长度为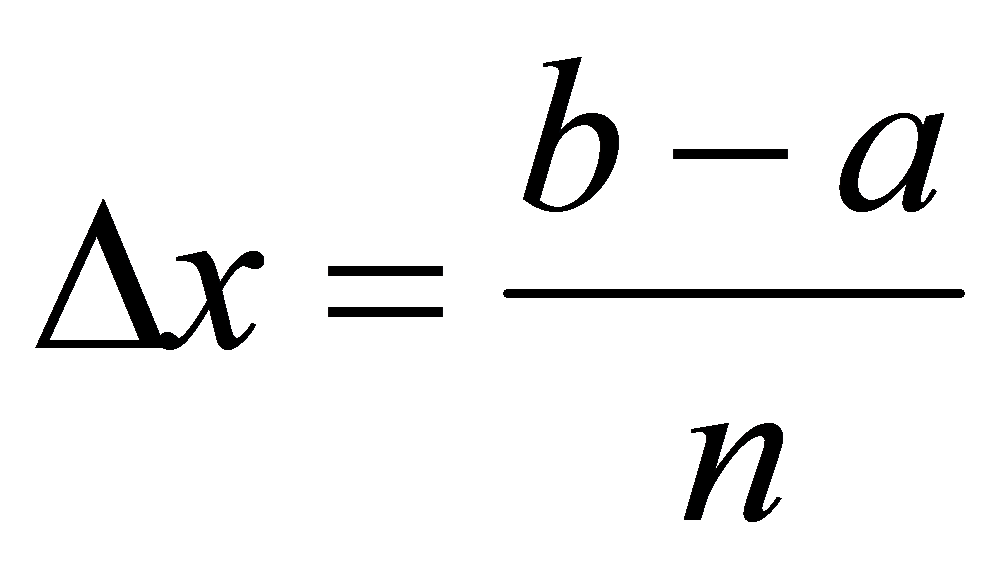，分点对应的函数值为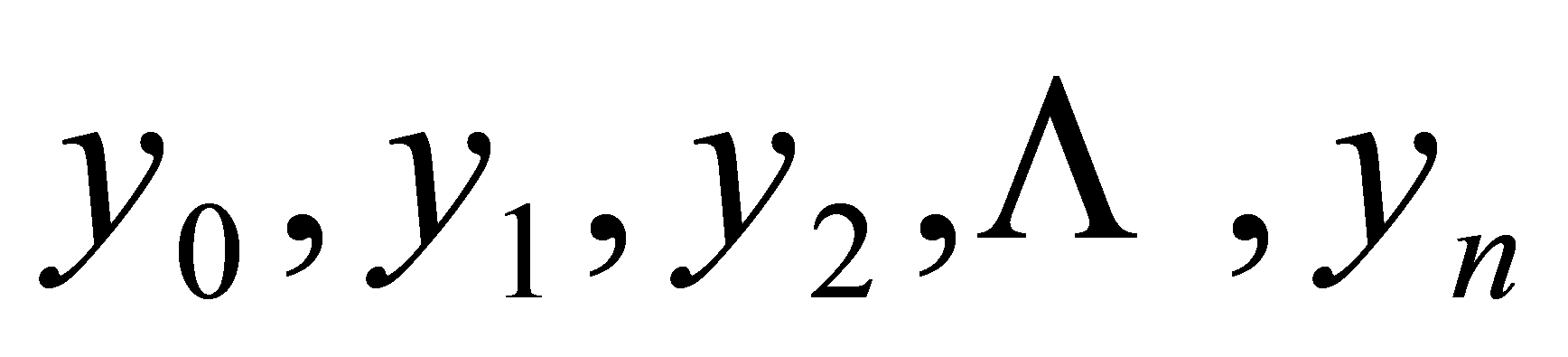，连接曲线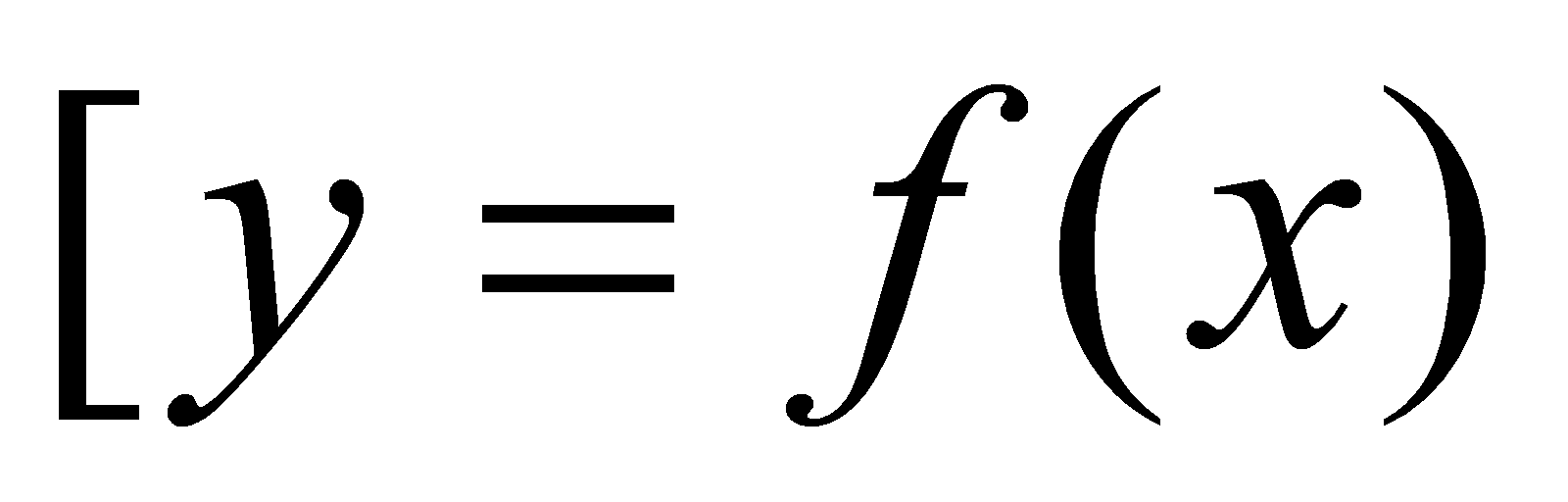上相邻两点，得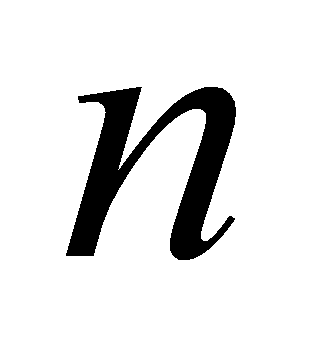个小直角梯形，如图5-10，

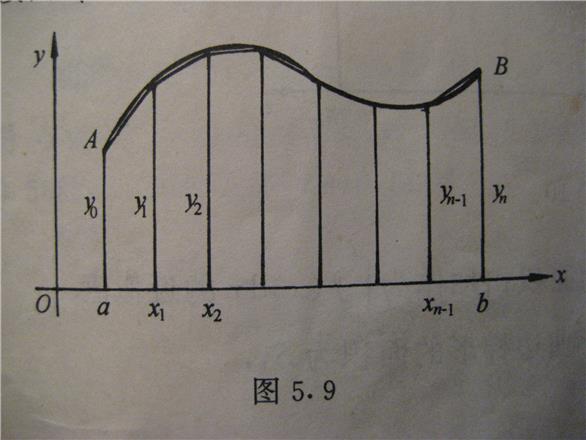
图5-10

它们的面积为

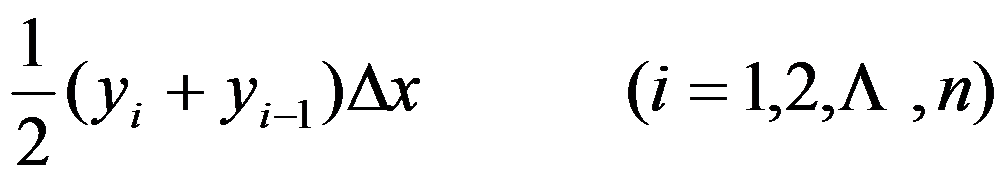
相加便得定积分的近似值

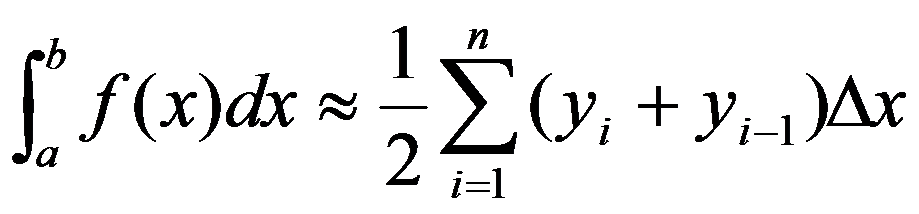
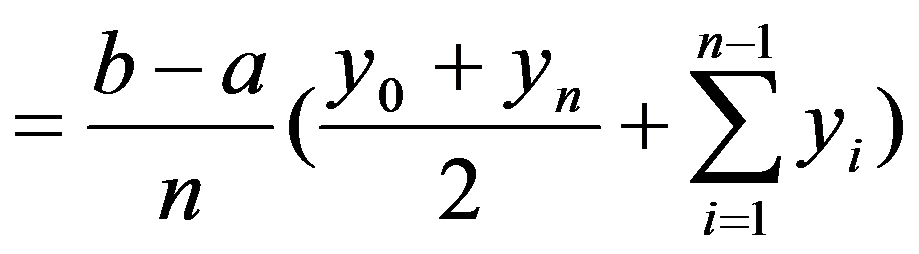
可以证明，若分点不均匀，则

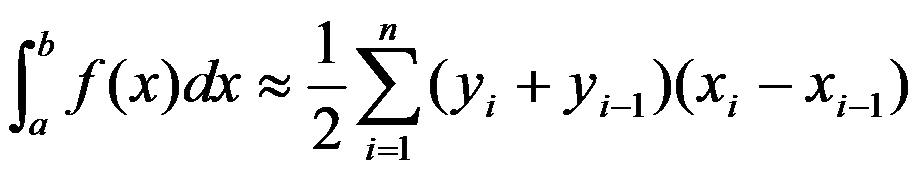
例5.3.13 有20名受试者各口服磷霉素2g，测得血液浓度平均值如下：

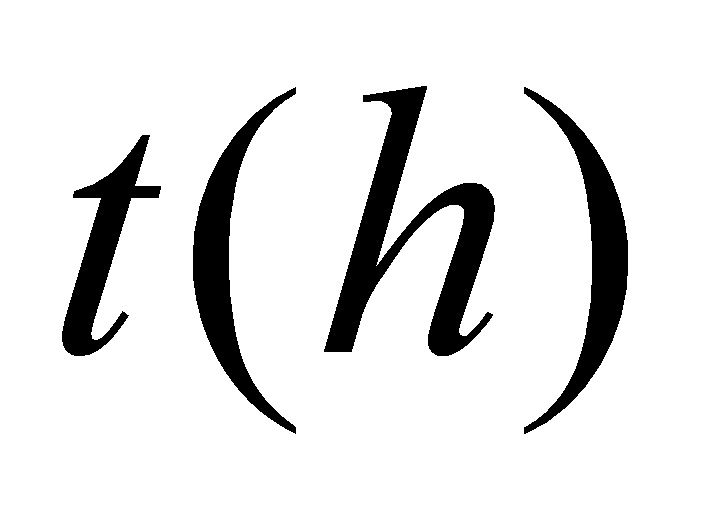
	0.5	1	2	4	6	8	12
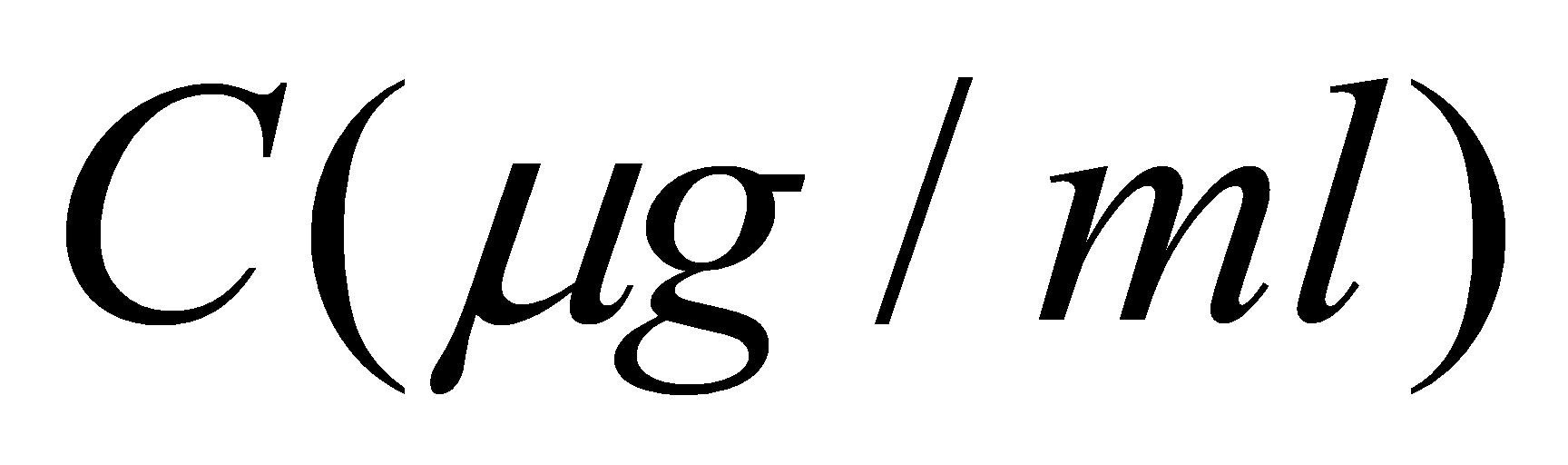
	1.00	4.54	8.89	6.44	3.69	2.87	2.23

计算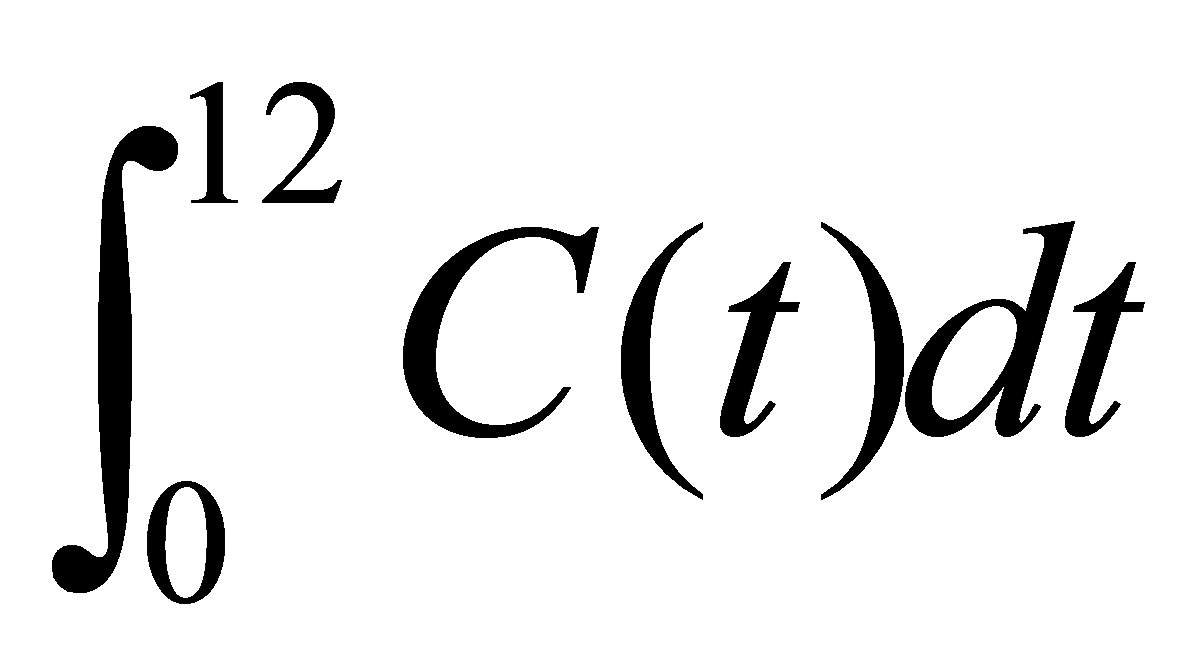的近似值。

解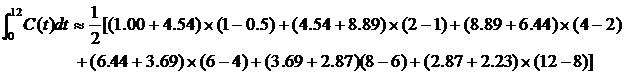

。

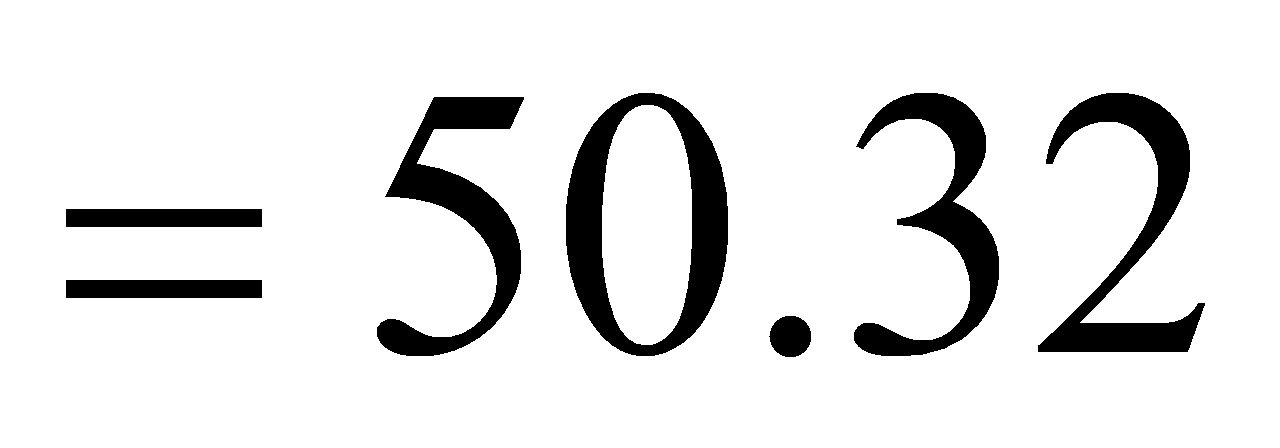(3)抛物线法（parabolic method）

抛物线法的基本思想是：用以抛物线为顶的小曲边梯形的面积来代替原来的小曲边梯形的面积。

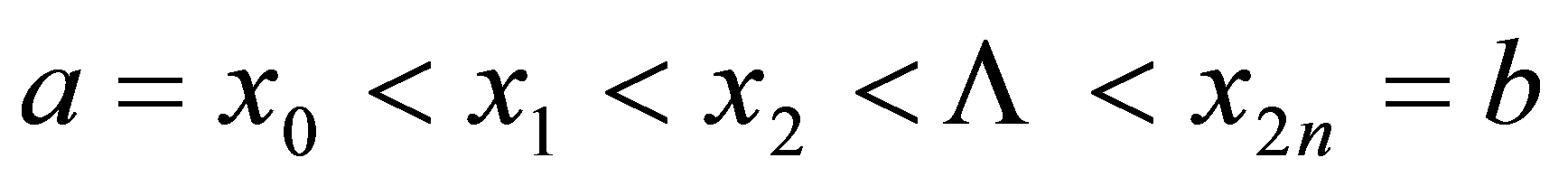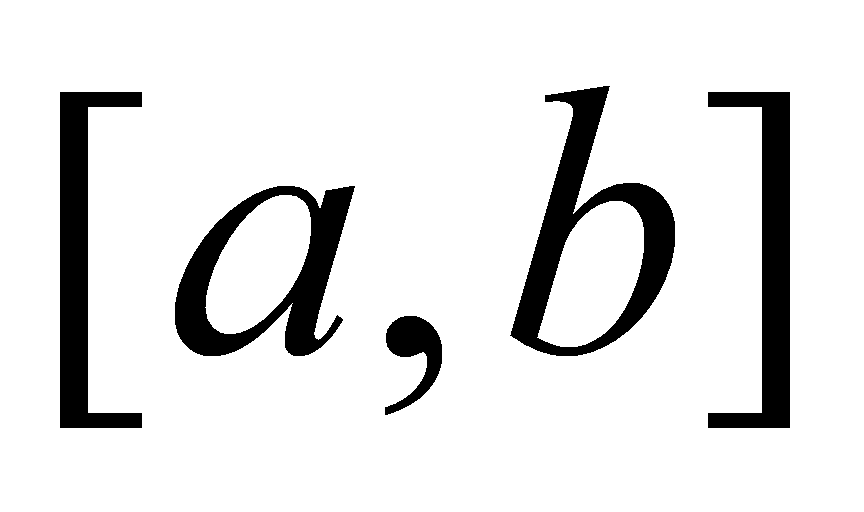用分点把区间分成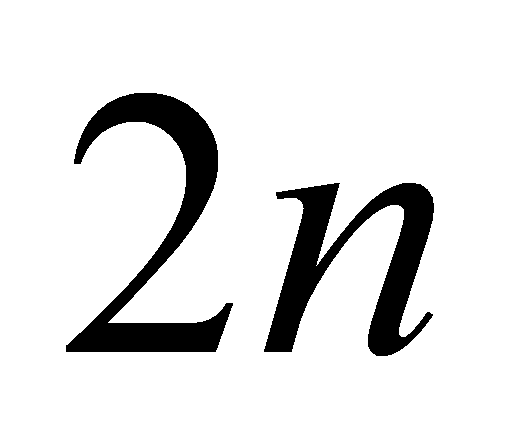等分，分点的函数值为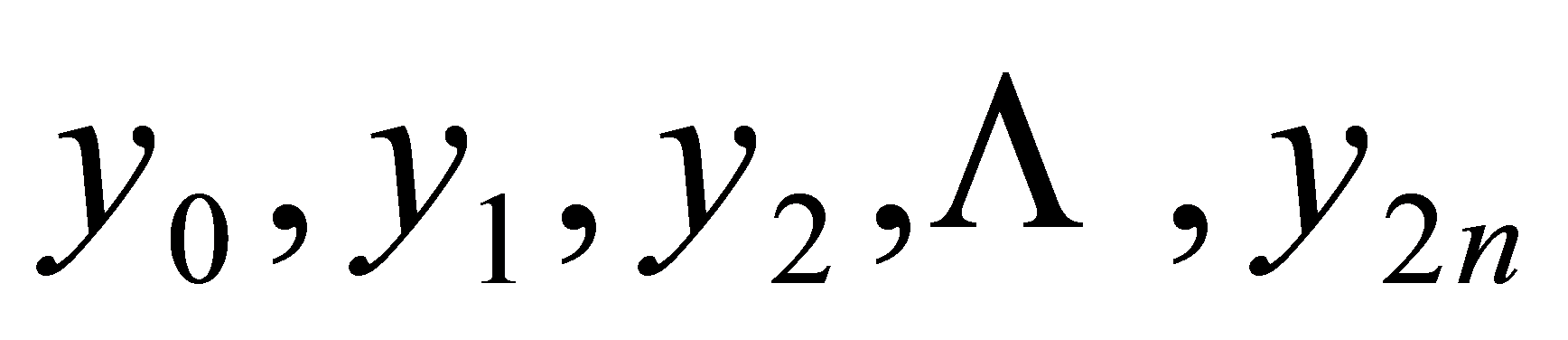，过各分点作平行于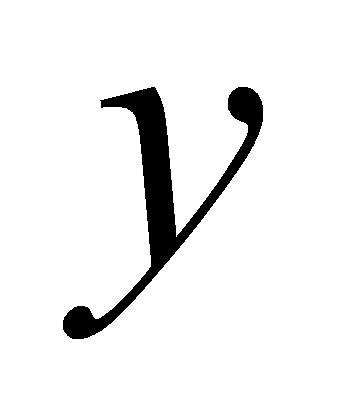轴的直线与曲线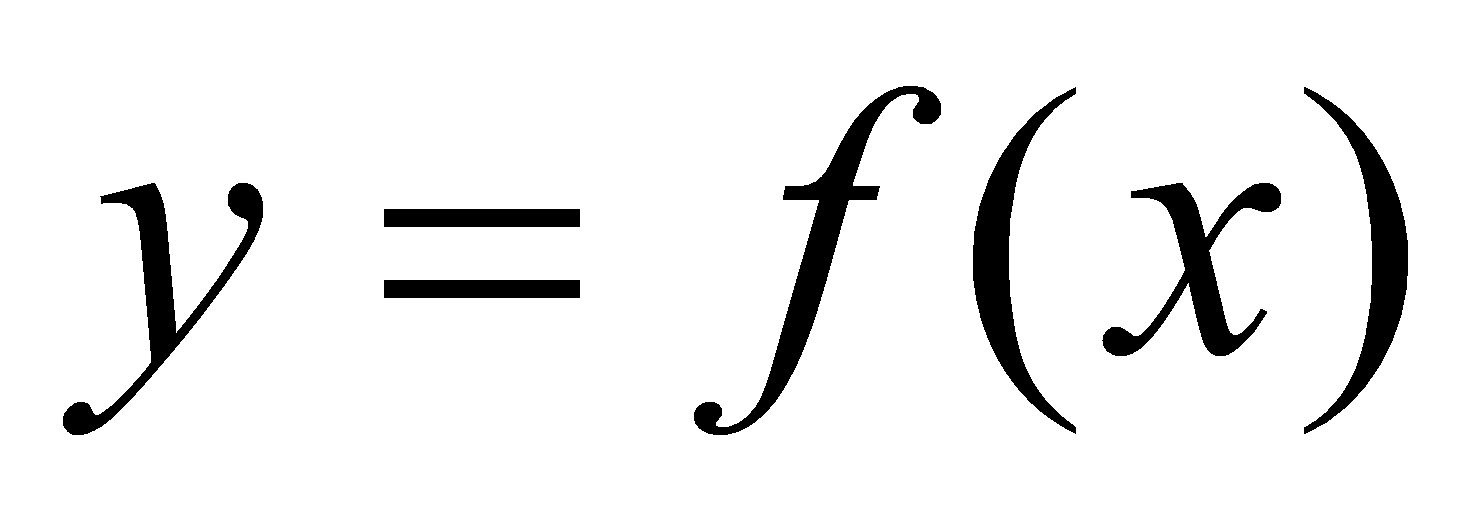相交于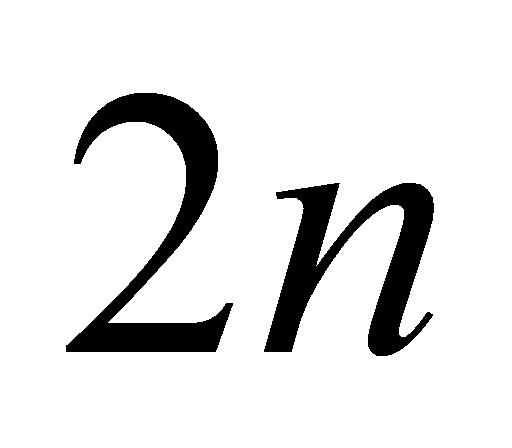个点，依次过相邻3个交点各作一条抛物线，如图5-11。

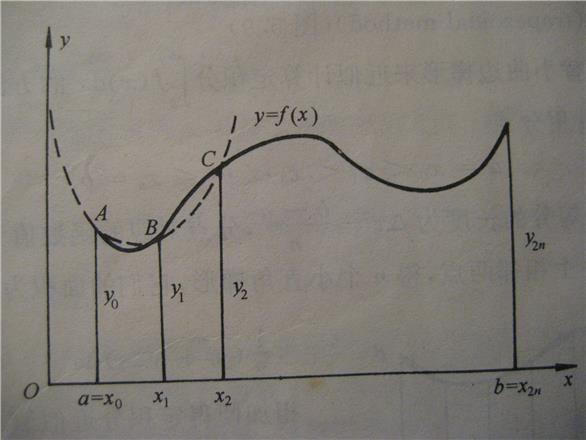
图5-11

将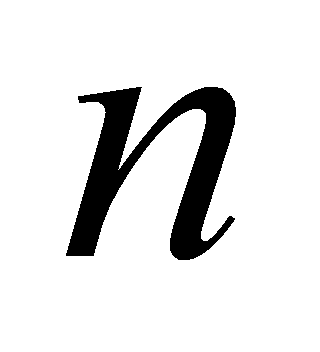个以抛物线为顶的小曲边梯形的面积相加作为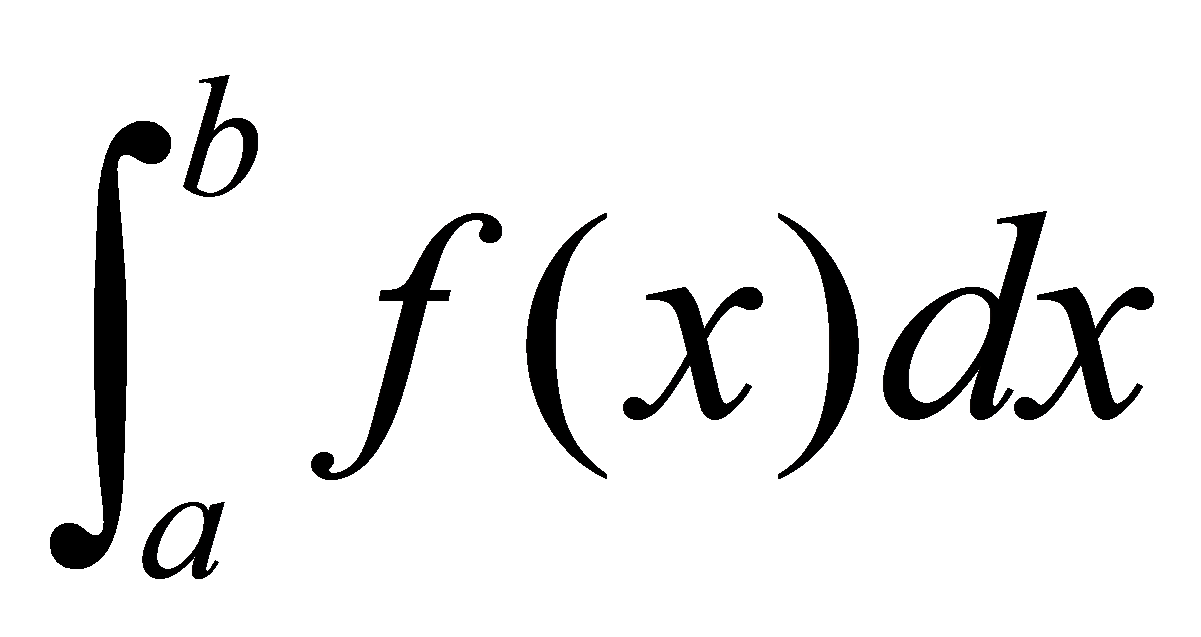的近似值。

例如，过前3点、、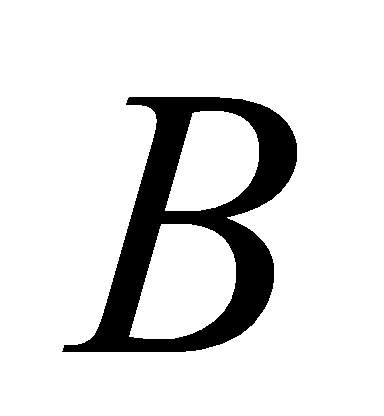的抛物线下小曲边梯形的面积为，

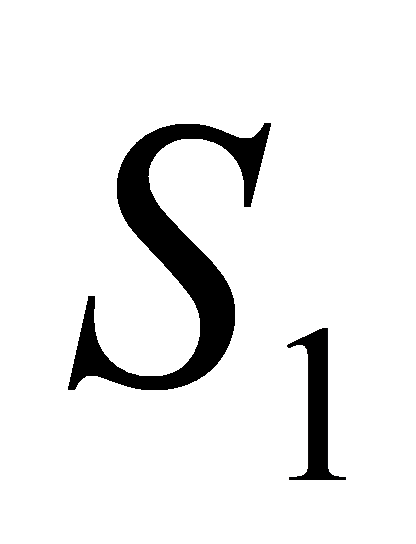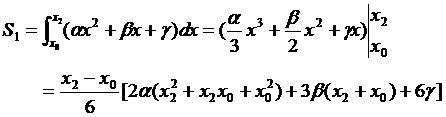
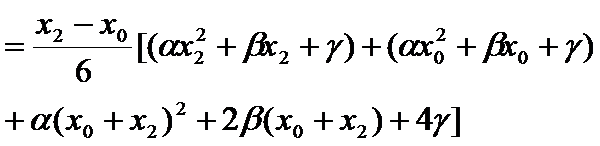
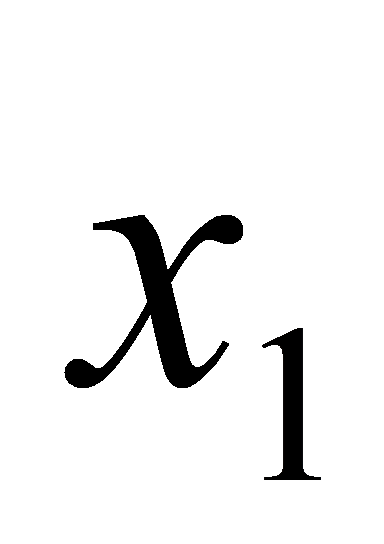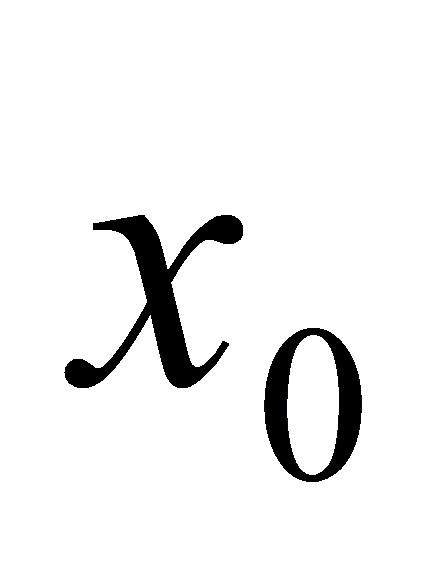由于是和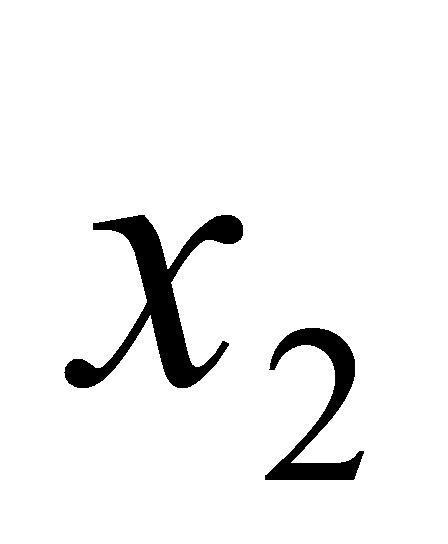的中点，所以，。

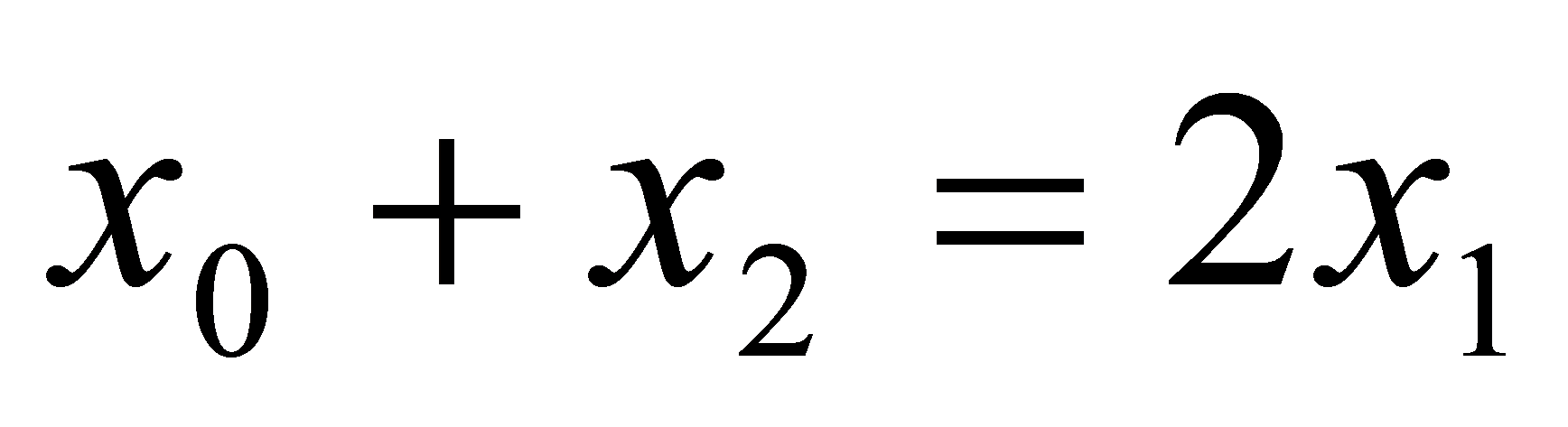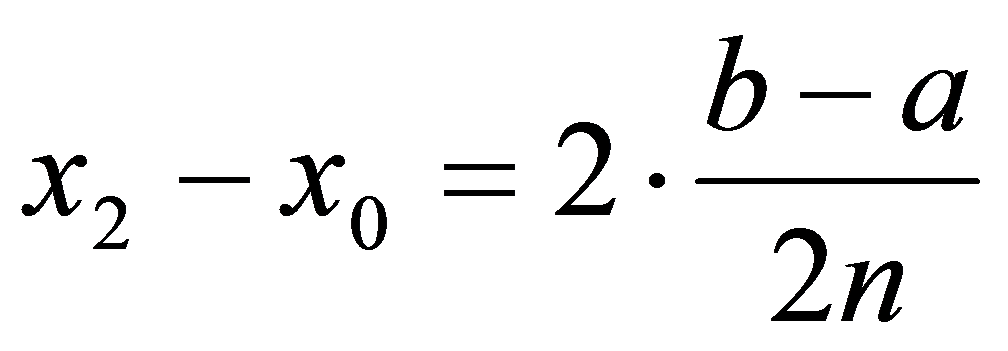从而 。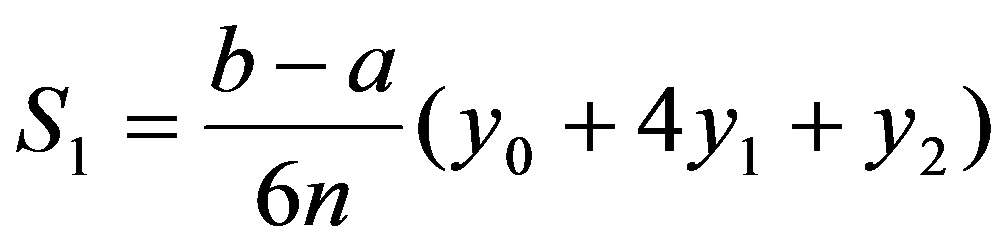

类似地可计算其它以抛物线为顶的小曲边梯形的面积为：

……

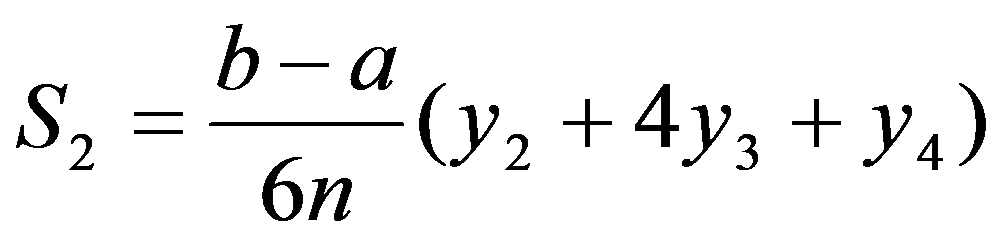
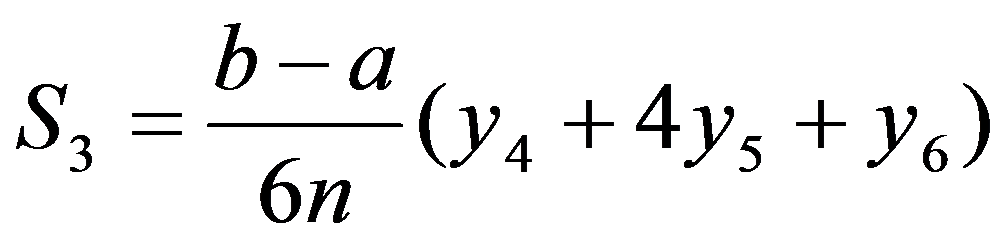
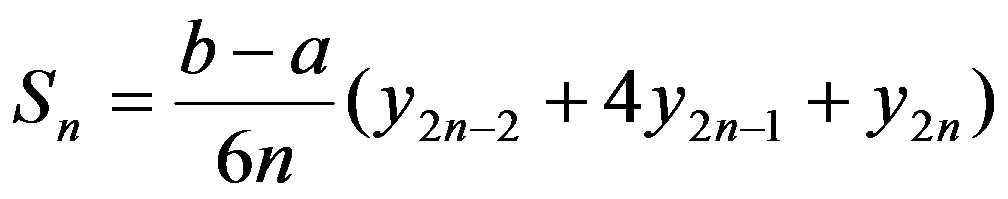
将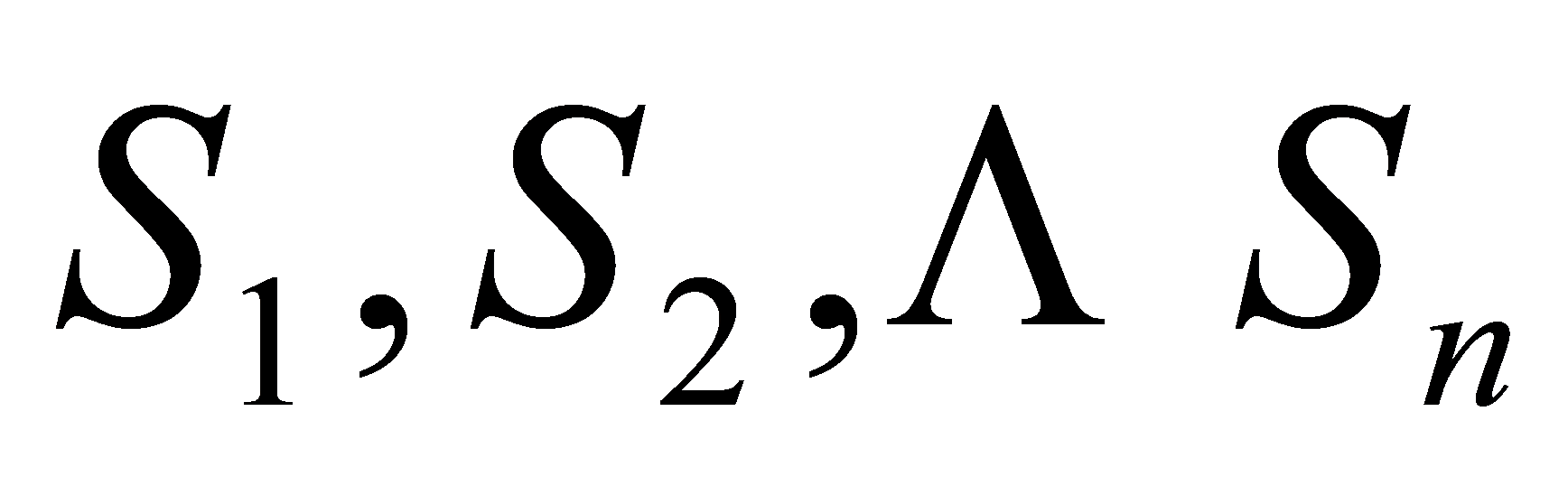加起来，就得到近似公式

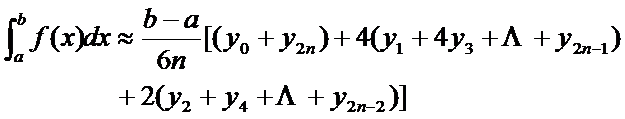
这个公式称为辛普生公式（）.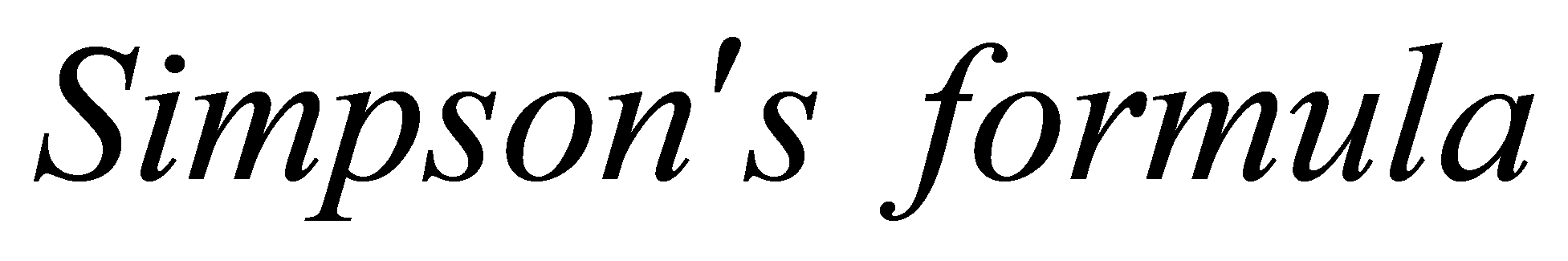

例5.3.14 分别用矩形法、梯形法和抛物线法计算定积分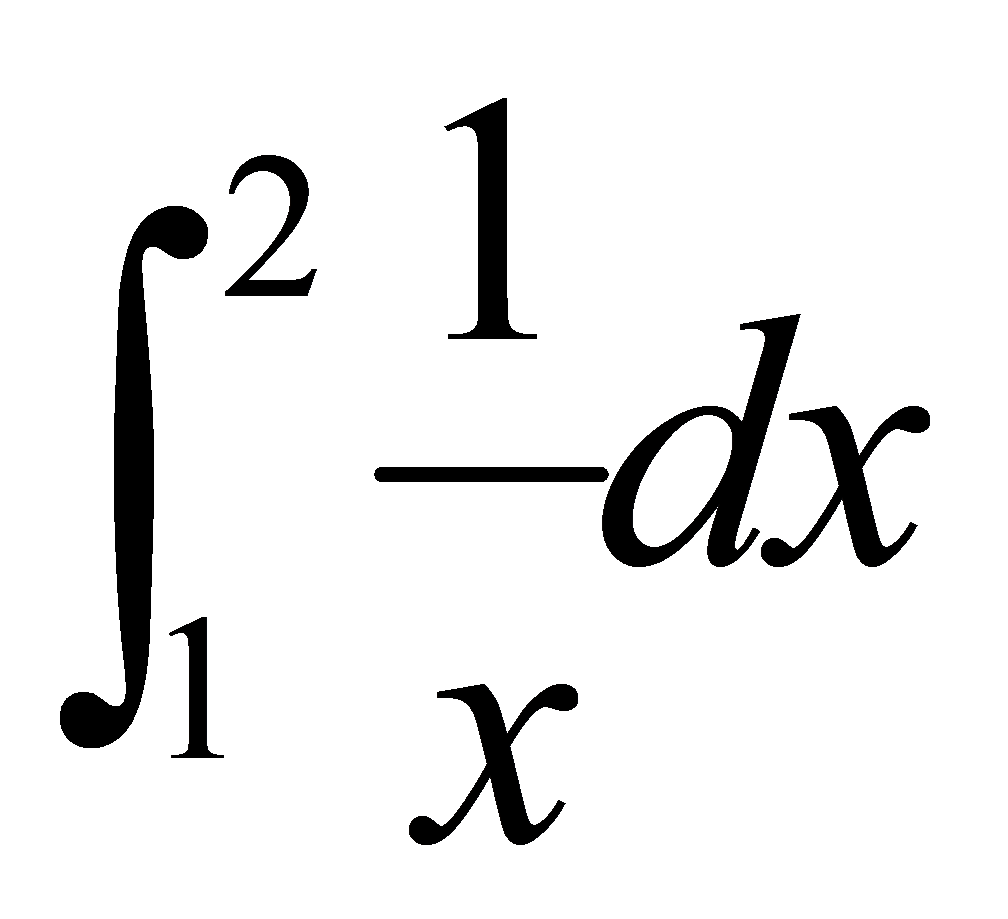的近似值，并比较它们的精确度。

解。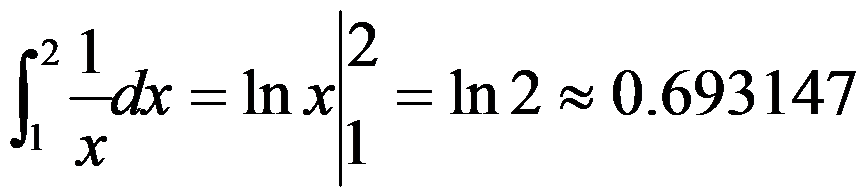

将积分区间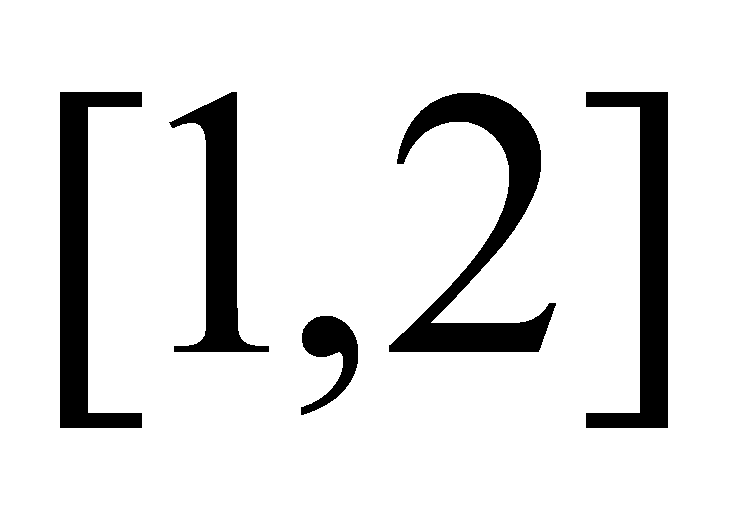10等分，即，令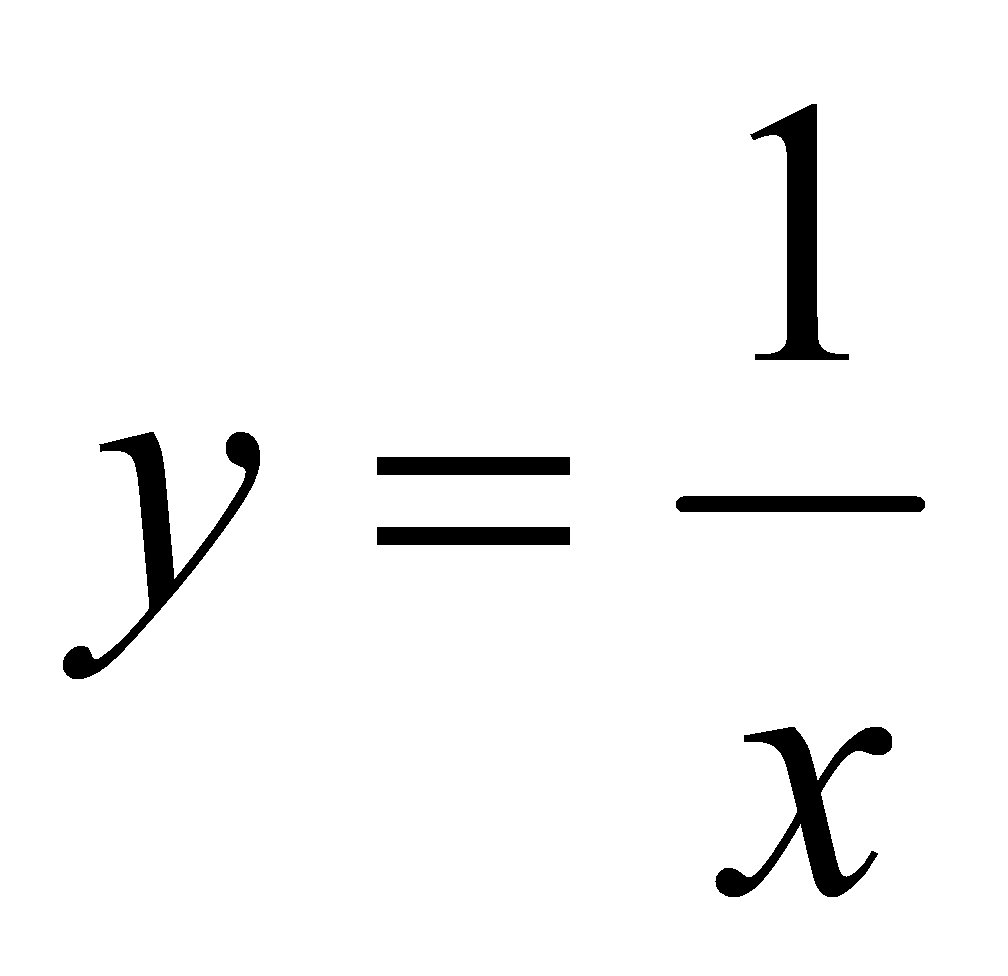，算得各个分点的函数值分别为1.000,0.9091,0.8333,0.7692,0.7143,0.6667,0.625,0.5882,0.5556,0.5263,0.5000。

矩形法：

。

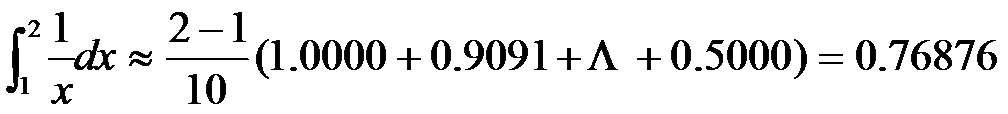梯形法：

。

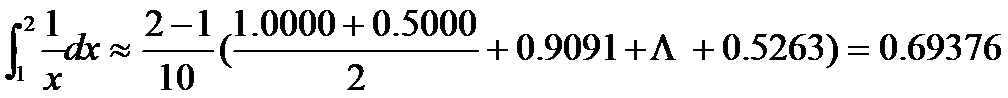抛物线法：

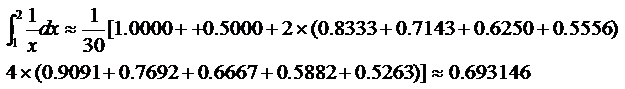
三种求法的近似值与0.693147比较，可知矩形法的精确度最低，其次是梯形法，抛物线法最好。